6. Útrapy mladých umelcov vzorové riešenie

Zadanie

Justína sa v posledom čase cítila priam uchvátená majstrovskými kúskami antických hrnčiarov. Keďže umenie jej nie je cudzie, rozhodla sa, že vezme veci (a hlinu) do vlastných rúk a niečo si sama vyrobí. Chcelo to trochu cviku a trpezlivosti, ale nakoniec sa jej podarilo vyrobiť dokonalú nádobu, ktorej prierez sa dá popísať rovnicou \[ y = L+\frac{x^2}{20L} - L\cos{\frac{x}{L}}\text{,} \] kde \(x\in\left<-6L;6L\right>\). Jej dielo ju tak tešilo, že si na dno uložila svoj obľúbený hmotný bod. Potom ale prišiel Kvík a potiahol nádobu vo vodorovnom smere so zrýchlením \(a\), až sa hmotný bod z nádoby vysypal. Justína nebola nadšená a hneď začala Kvíkovi vysvetľovať, že musí ťahať zrýchlením takým a takým, aby jej drahý hmotný bod nevysypal. Pre aké hodnoty \(a\) to platí?

V tejto úlohe od vás nepožadujeme úplne presný (t. j. analytický) výsledok.

Začnime najprv technikalitami. Keďže je nádoba symetrická, stačí sa obmedziť iba na pohyb do jedného smeru a skúmať, aké hodnoty môže nadobúdať veľkosť zrýchlenia. Minimálne zrýchlenie je úplne jasné, jeho hodnota je \(a_{\mathrm{min}} = 0\). Stačí nám preto nájsť hodnotu maximálneho zrýchlenia \(a_{\mathrm{max}}\), pri ktorom ešte hmotný bod z nádoby nevyletí.

K samotnému riešeniu možno pristupovať dvoma spôsobmi. Prvý, ťažký prístup, by bolo riešiť úlohu cez sily. V každom bode funkcie, ktorá popisuje nádobu, by sme museli vypočítať výslednicu gravitačnej a normálovej sily pôsobiacej na hmotný bod a následne hľadať podmienky stability… jednoducho fuj! Druhý, v tomto prípade stráviteľnejší prístup, vedie cez energie. Aj keď teraz to má malý háčik. Na prvý pohľad nevieme, akú energiu má zrýchľujúci hmotný bod. No keď sa na problém pozrieme (doslova) z iného uhla, môžeme si všimnúť, že zrýchľovanie vo vodorovnom smere spôsobuje pre hmotný bod efektívne gravitačné zrýchlenie veľkosti \[ g_{\mathrm{eff}} = \sqrt{g^2 + a^2} \text{,} \]

natočené pod uhlom \[ \alpha = \arctan\frac{a}{g} \]

oproti pôvodnému smeru.

Toto pozorovanie spolu s poznatkom, že všetky systémy minimalizujú svoju energiu, nás vedú k odpovedi na otázku, aká je hodnota \(a_{\mathrm{max}}\). No je presne taká, že v natočenej súradnicovej sústave o uhol \(\alpha\) prestáva pre hmotný bod existovať potenciálova jama v nádobe, ktorá by ho zadržala. Inak povedané, bude to vtedy, keď sa v natočenej sústave stane pôvodný bod \([0;0]\) tým „najvyšším“ bodom nádoby.¹

Ako to teraz vypočítať? Keďže zadanie od nás nechce presný analytický výsledok, ukážeme si dva spôsoby, pri ktorých si pomôžeme múdrymi programami. Prvý spôsob je úplne bežný a druhý je pre fajnšmekrov, ktorí už majú isté skúsenost s deriváciami.

Binárne vyhľadávanie v grafickom programe

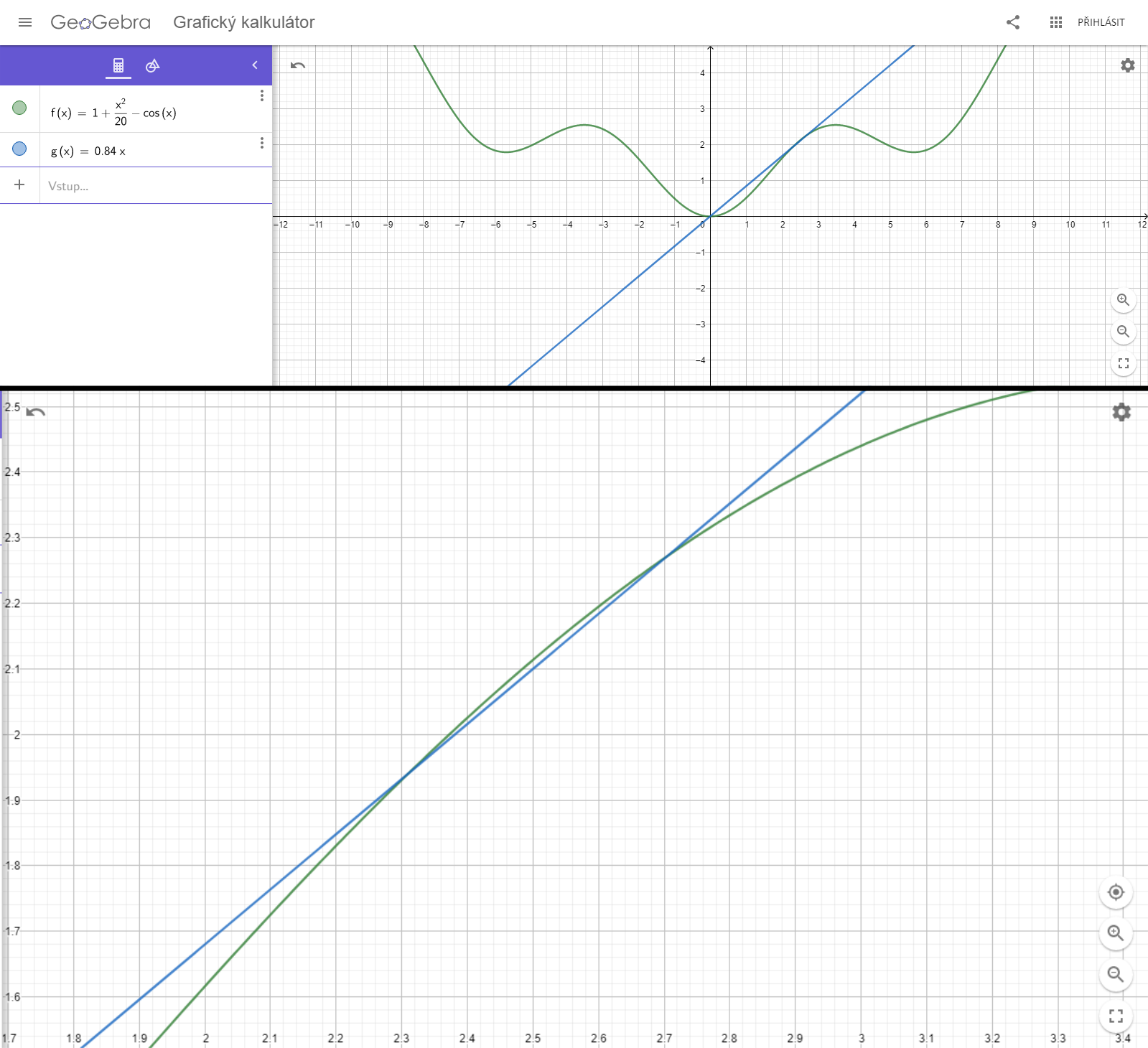
Z toho, čo bolo povedané, by malo byť jasné, že v pôvodnej súradnicovej sústave vieme hladinu nulovej energie zrýchľujúceho bodu popísať priamkou \(\frac{a_{\mathrm{max}}}{g} x\). Teraz nám stačí nájsť iný ako nulový priesečník s krivkou popisúcou nádobu. Teda riešime rovnicu \[ L +\frac{x^2}{20L} - L\cos{\frac{x}{L}} = \frac{a_{\mathrm{max}}}{g} x \] pre zrýchlenie \(a_{\mathrm{max}}\).

Je to však rovnica o dvoch neznámych \(x\) a \(a_{\mathrm{max}}\). Nezostáva nám nič iné, iba vykresliť si obe krivky v nejakom grafickom programe, napríklad GeoGebre, a meniť parameter \(a_{\mathrm{max}}\), až po kým sa krivky nebudú dotýkať iba v jednom bode. Samozrejme, nejde to robiť inak ako formou pokus–omyl, prípadne binárnym vyhľadávaním medzi hodnotami, kde sa krivky pretínajú v dvoch bodoch alebo sa nepretínajú vôbec.

Postupným iterovaním dostaneme hodnotu \(a_{\mathrm{max}} \doteq \num{0.845}\,g\). A tým je úloha vyriešená.

Hľadanie lokálneho maxima

Na úlohu sa možno pozrieť aj tak, že bod, v ktorom sa krivky dotýkajú, má byť lokálnym maximom v otočenej sústave, respektíve má byť maximom vzhľadom na priamku \(\frac{a_{\mathrm{max}}}{g} x\). To znamenená, že budeme derivovať a hľadať maximum, no treba si dať pozor na to, ako do toho zakomponovať podmienku s priamkou. To je však pomerne jednoduché, ten dotýkajúci sa bod musí byť maximom, aj keď od pôvodnej funkcie odčítame funkciu priamky. Máme teda dve rovnice o dvoch neznámych \[ L + \frac{x^2}{20L} - L\cos{\frac{x}{L}} - \frac{a_{\mathrm{max}}}{g} x = 0 \text{,} \] \[ \frac{x}{10L} + \sin{\frac{x}{L}} -\frac{a_{\mathrm{max}}}{g} = 0 \text{.} \]

To analyticky nespočítame, tak to dáme do nejakého múdreho programu, napríklad Wolframu Alpha alebo Mathematicy a dostaneme výsledok \(a_{\mathrm{max}} \doteq \num{0.84546}\,g\), čo je v zhode s tým predchádzajúcim.