5. Pôjde ti karta vzorové riešenie

Zadanie

Po úspešnom postavení a zdokumentovaní šesťposchodovej pyramídy z karát si Adam povedal, že jeho úroveň stavania kartových domčekov by mohla byť ešte vyššia. Ďalším levelom by bolo zahrnutie cudzích predmetov do štruktúry vežičky. Napríklad taký valček by mohol byť celkom výzva.

Aby Adam otestoval svoj nápad, zobral si valček hmotnosti \(m\) a položil naň kartu, ktorá s podložkou zvierala uhol \(\alpha\). Koeficient statického trenia \(f\) medzi valčekom a podložkou a medzi valčekom a kartou bol rovnaký. Aký najmenší mohol byť, aby sa valček spod karty nevyšmykol? Predpokladajte že trenie medzi kartou a podložkou je dostatočné na to, aby sa karta na podložke nezošmykla.

Úlohy na statiku sú veľmi často iba technickým výpočtom. Keď raz pochopíme, ako sa také veci počítajú, už nás nezvyknú prekvapiť. Otázky zvyknú byť vždy formulované tak, že hľadáme „najmenší koeficient trenia“, „najväčšiu hmotnosť“, „najmenší uhol“ a podobne. V praxi to znamená: uvedomme si, že veľkosť trecej sily je \(F_t\leq Nf\), kde \(N\) je veľkosť normálovej sily, ktorou podložka podopiera objekt. Napríklad keď položíme mobil na knižku a postupne knižku nakláňame, trecia sila sa zväčšuje až po hranicu \(F_t=Nf\), kedy dosiahne maximum a pri zväčšení uhla náklonu sa začne mobil zošúchavať. Pri statických úlohách zvykneme študovať práve takúto hranicu medzi stavom, kedy sú objekty stabilné, a stavom, kedy sa začnú pohybovať.

Na hranici uvažujeme ešte stabilný stav – všetky sily v smere \(x\) a smere \(y\) sú v rovnováhe a objekty sa neotáčajú (t.j. celkový moment sily je nulový). Skúmame pohyb valčeka, teda si nakreslíme všetky sily, ktoré naň pôsobia: tiažová veľkosti \(mg\) zvislo nadol, normálová od podložky veľkosti \(N\) zvislo nahor, trecia sila od podložky v smere proti šmyku veľkosti \(F_{t1}\), sila od karty veľkosti \(F\) pôsobiaca kolmo na valček a trecia sila smere proti šmyku karty z valčeka veľkosti \(F_{t2}\).

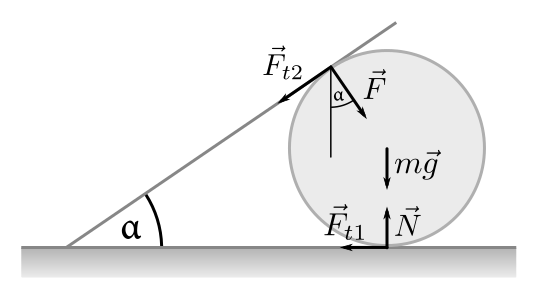
Ak je celkový moment sily nulový, je jedno, vzhľadom na ktorý bod ho počítame. My budeme počítať na stred valčeka s polomerom \(r\), keďže vtedy silový moment od síl \(\vec{F}\), \(\vec{N}\) a \(\vec{F_g}\) je nulový (rozmyslite si, že prečo!), čo zjenoduší podmienku iba na \[ rF_{t2}=rF_{t1}\text{.} \]

Vidíme, že veľkosti trecích síl v rovnováhe sú rovnaké, označme si ich \(T\). Teraz si rozložíme sily do smerov \(x\) a \(y\) a napíšeme podmienky stability. Pre \(y\)-smer platí \[ N-mg-\underbrace{F\cos\alpha}_{F_y}-\underbrace{T\sin\alpha}_{T_{2y}}=0 \]

a pre \(x\)-smer platí \[ -T+\underbrace{F\sin\alpha}_{F_x}-\underbrace{T\cos\alpha}_{T_{2x}}=0\text{.} \]

Stále nevieme veľkosť trecej sily. Z ostatných dvoch rovníc ju vylúčime a s pomocou \(\cos^2x+\sin^2x=1\) dostávame hodnotu normálovej sily \(N\) \[ N=mg+F\text{.} \]

Dostali sme, že veľkosť sily \(N\) je väčšia ako veľkosť sily \(F\). Pri myslenom zmenšovaní koeficientu \(f\) sa valec začne šúchať o kartu, a nie o podložku. Je to zrejmé z toho, že hranica šmyku, kedy trecia sila má rovnakú veľkosť ako súčin koeficientu trenia a normálovej sily, nastane skôr pri menšej normálovej sile \(F\). Pre hraničný prípad smelo dosadzujeme \(T=fF\) a z rovnice pre \(x\)-smer dostávame výsledok \[ f=\frac{\sin\alpha}{1+\cos\alpha}=\tan{\frac{\alpha}{2}}\text{.} \]

Ten platí bez ohľadu na hmotnosť valčeka a karty. Predpokladáme, že karta je dostatočne dlhá na to, aby bola dotyčnicou ku valčeku, ale dostatočne krátka, aby ju ťažisko nepreklopilo. Rovnako ako je na obrázku v zadaní. V riešeniach sme hodnotili aj argument, prečo sa valček začne šmýkať pri karte, ale nie pri podložke.