6. Sklíčka dotykov vzorové riešenie

Čo robí taká šošovka? Šošovka sa skladá. Z? Materiálu. A ako asi viete, z rôznych dôvodov sa v materiáloch svetlo pohybuje pomalšie ako vo vákuu. A keďže svetlo sa vždy chce dostať z jedného miesta na druhé za najkratší čas¹, spôsobí to, že lúč svetla na rozhraní dvoch materiálov zabočí. To je zákon lomu. Šošovky ale majú taký špeciálny tvar, že lúče, ktoré prichádzajú z jedného bodu, sa zlomia presne tak, že v jednom bode aj skončia. To je princíp zobrazenia v optickej sústave. A existujú aj opačné šošovky, ktoré lúče z jedného bodu zlomia tak, že stále budú vyzerať, ako keby prichádzali z jedného bodu, ale bližšieho. To je celé poslanie šošoviek.

To, ako veľmi šošovka láme svetlo, teda aká je silná, nám určuje ohnisková dĺžka \(f\). Čím kratšia ohnisková dĺžka, tým silnejšia šošovka a tým viac láme svetlo. Niektorí ľudia ale majú problém s tým, keď menšie číslo znamená niečo silnejšie. Našťastie pre nich, tento problém má jednoduché riešenie a to, že si vymyslíte aj veličinu \(1/f\). Tak aj urobili, nazvali ju optická mohutnosť s jednotkou dioptria a majú. Takže okuliare s 5 dioptriami majú ohniskovú dĺžku \(\SI{20}{\centi\metre}\).

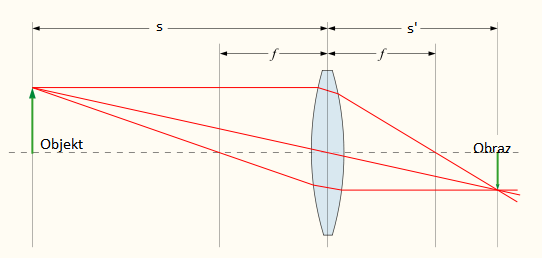
Asi by bolo dobré zistiť, kde tie lúče vlastne skončia. Ak budú lúče vychádzať z bodu vo vzdialenosti \(s\) od šošovky s ohniskovou vzdialenosťou \(f\), v akej vzdialenosti \(s'\) od šošovky bude bod, v ktorom sa stretnú? S trochou geometrie sa dá odvodiť celkom jednoducho: \[ \frac{1}{s}+\frac{1}{s'}=\frac{1}{f}\text{.} \]

Vzdialenosti sú vyznačené aj na tomto obrázku:

Riešenie

Po úvodnej reči sa môžeme konečne pustiť do riešenia. Čo znamená “nahradiť sústavu”? Asi to, že chceme, aby nová šošovka zobrazila každý predmet do toho istého miesta, ako dve staré šošovky. Tak si to napíšme. Poloha obrazu po prejdení prvou šošovkou bude \[ s_1'=\frac{s _1f_1}{s _1-f_1}\text{.} \]

Tento obraz môžeme použiť ako zdroj pre ďalšiu šošovku, keďže tá samozrejme netuší, či sa pozerá na skutočný objekt, alebo na obraz vytvorený inou šošovkou: \[ s_2'=\frac{(d-s _1')f_2}{d-s _1'-f_2}\text{.} \]

\(s_1'\) dosadíme do druhej rovnice: \[ s_2' = \frac{f_2 \left(d-\frac{f_1 s_1}{s_1-f_1}\right)}{d-\frac{f_1 s_1}{s_1-f_1}-f_2}\text{.} \qquad(1)\]

Teraz by sme chceli, aby táto sústava bola ekvivalentná sústave s jednou šošovkou. Avšak ukazuje sa tu jeden problém. Ak by sme uvažovali, že nová šošovka je tenká a nachádza sa vo vzdialenosti \(\delta_1\) od prvej šošovky, potom by bola vzdialenosť novej od druhej šošovky rovná \(\delta_2=d-\delta_1\text{.}\) Avšak dá sa ukázať, že ohnisková vzdialenosť a pozícia by v takomto prípade závisela od polohy predmetu. Toto si ukážeme neskôr. Záverom, tenká šošovka ekvivalentná pôvodnej sústave neexistuje.

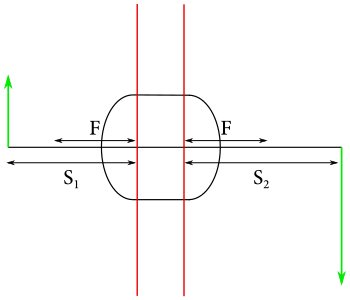
Avšak v optike existuje koncept takzvaných hlavných rovín. Predstavte si, že z nejakého dôvodu by neplatila iba “obyčajná” zobrazovacia rovnica \(\frac{1}{s}+\frac{1}{s'}=\frac{1}{f}\), kde vzdialenosti \(s\) a \(s'\) sú merané od šošovky. Ale platila by aj upravená verzia, veľmi podobná tej obyčajnej, len s tým rozdielom, že vzdialenosti \(s\) a \(s'\) by sme nemerali od šošovky, ale od nejakých rovín, ktoré si nazveme “hlavné roviny”. Rovnica by potom mala tvar \[ \frac{1}{S_1}+\frac{1}{S_2}=\frac{1}{F}\text{,} \]

kde \(S_1\) a \(S_2\) sú vzdialenosti od prvej, resp. od druhej hlavnej roviny a \(F\) je vzdialenosť ohniskového bodu od hlavných rovín. Najväčšia vymoženosť toho je, že hlavné roviny nemusia byť totožné. Je to ako keby ste šošovku rozdelili na dve polovice, umiestnili by ste ich do nejakej vzdialenosti od seba, a potom sa tvárili, že svetlo sa medzi tymito dvoma polovicami “teleportuje”. Sranda je, že takto to naozaj funguje, že každá šošovka, či už hrubá alebo tenká, alebo nejaká optická sústava sa dá nahradiť nejakými hlavnými rovinami a nejakou výslednou ohniskovou vzdialenosťou \(F\). Takže ak určíte tieto parametre optickej sústavy, môžete ju nahradiť akoukoľvek inou optickou sústavou s rovnakými parametrami. My máme nahradiť sústavu len jednou šošovkou, takže musíme použiť šošovku, ktorá nemá totožné hlavné roviny. Bude to hrubá šošovka?

Predpokladajme, že hlavné roviny novej sústavy sú od seba vzdialené \(D\). Neuškodí to nášmu postupu, keďže ak by to tak nebolo, nakoniec by sme akurát došli k tomu, že \(D=0\). Ako sa ale ukáže, takto to nebude. Vzdialenosť prvej roviny a prvej pôvodnej šošovky nech je \(\delta_1\) a vzdialenosť druhej roviny od druhej pôvodnej šošovky nech je \(\delta_2\). Platí \(d=D+\delta_1+\delta_2\). Zobrazovacia rovnica novej šošovky je \[ \frac{1}{s_1 + \delta_1}+\frac{1}{s_2' +\delta_2}=\frac{1}{F}\text{,} \]

kde \(s_1\), \(s_2'\) sú staré vzdialenosti zo zobrazovacej rovnice dvoch tenkých šošoviek. Osamostatníme \(s_2'\): \[ s_2'=\frac{F (s_1 +\delta_1)}{s_1+\delta_1 -F}-\delta _2\text{.} \qquad(2)\]

Keďže požadujeme, aby táto sústava bola ekvivalentná pôvodnej sústave, \(s_2'\) zároveň musí vyhovovať rovniciRovnica 1. Máme dve rovnice a tri neznáme, ktoré musia ale platiť pre všetky hodnoty parametra \(s_1\). Nie veľmi nádejná situácia. Avšak my sa pokúsime vynájsť. Vieme, že rovnobežný lúč sa zobrazí do ohniska novej sústavy. Toto korešponduje so situáciou, kedy je predmet v nekonečne, takže v limite \(s_1 \to \infty\) rovnicaRovnica 2 prejde na \[ s_2'=F-\delta_2\text{.} \]

Podobne, ak by sme vyjadrili nie \(s_2'\) ale \(s_1'\) a urobili limitu \(s_2 \to \infty\), dostaneme \[ s_1'=F-\delta_1\text{.} \]

Ak spočítame rovnakú limitu pre \(s_2'\) respektíve \(s_1'\) z rovniceRovnica 1, s využitím predchádzajúcich dvoch limitných vzťahov dostaneme \[ F=\frac{f_1 f_2- f_2 d}{f_1+f_2 -d} + \delta_2\text{,} \qquad(3)\]

\[ F=\frac{f_1 f_2- f_1 d}{f_1+f_2 -d} + \delta_1\text{.} \qquad(4)\]

Poslednú rovnicu získame z faktu, že lúč predmetu umiestneného priamo v ohnisku prvej šošovky pôvodnej sústavy sa zobrazí do ohniska druhej šošovky. Teda ak \(s_1=f_1\), potom \(s_2'=f_2\). Po dosadení doRovnica 2 získame:

\[ f_2=\frac{F(f_1+\delta_1)}{f_1+\delta_1-F}-\delta_2\text{.} \qquad(5)\]

Z týchto rovnícRovnica 3,Rovnica 4,Rovnica 5 dokážeme vyjadriť ohniskovú vzdialenosť novej sústavy a vzdialenosti hlavných rovín.² \[ F=\frac{f_1 f_2}{f_1+f_2-d}\text{,} \] \[ \delta_1=\frac{d f_1}{f_1+f_2-d}\text{,} \] \[ \delta_2=\frac{d f_2}{f_1+f_2-d}\text{.} \]

Hneď postrehneme niekoľko vecí. V prvom rade neplatí všeobecne, že \(\delta_1+\delta_2\) by sa rovnala \(d\), čiže \(D \neq 0\text{.}\) Takže tým sa opodstatňuje použitie hlavných rovín. Poznámka na záver. Aby náš dôkaz bol korektný, potrebovali by sme ukázať, že riešenia ktoré sme našli naozaj vyhovujú všetkým hodnotám parametra. Toto sa dá urobiť spätným dosadením nájdených riešení. Vskutku to vyjde, môžete sa presvedčiť.

Na záver necháme vo vzduchu visieť otázku, či ku každej dvojici hlavných rovín existuje skutočná šošovka. Po chvíli zamyslenia by sme mohli uveriť tomu, že to tak naozaj je. Uvedomme si, že môžeme voliť polohu ekvivalentnej šošovky, takže to, čo nás v skutočnosti zaujíma, je iba vzájomná vzdialenosť hlavných rovín a nie ich skutočná poloha voči šošovke. Vzhľadom na to, že tenká šošovka má splývajúce hlavné roviny (\(D=0\)), musíme hľadať medzi hrubými šošovkami. Poloha hlavných rovín hrubej šošovky závisí okrem iného aj na jej hrúbke³, takže na to, aby sme našli šošovku s požadovanou vzdialenosťou hlavných rovín, stačí zvoliť správnu hrúbku šošovky.