7. Fajnšmeker vzorové riešenie

Prostriedky a obmedenia udávané zadaním nám toho neumožňujú robiť veľa. S vodami napríklad nemusíme nič robiť, čo nám dáva prvý odhad \(T_{\mathrm{max}} = \SI{0}{\celsius}\). Tento postup však nevyčerpal veľkodušnosť zadania, ktoré nám dovoľuje dať obe vody do tepelne vodivého kontaktu. Ako nás asi učili, teplota je taká vec, že keď k sebe priložím dve veci, ktoré ju majú rovnakú, nič zaujímavé sa neudeje. Ak ju však majú rôznu, po istom čakaní ju už rôznu mať nebudú. Vieme tiež, že ak sú k sebe prikladané veci z rovnakej látky, čo naše vody prakticky sú, túto novú, kompromisnú teplotu zistíme ako množstvom vážený priemer pôvodných teplôt. Viacej nám ani netreba.

Priložme teda vody k sebe. Použitím pred chvíľou osviežených vedomostí dospejeme k tomu, že takto pre destilovanú vodu dosiahneme \(T_{\mathrm{max}} = \SI{50}{\celsius}\). Toto zlepšenie je výrazné, nám však stále ostáva posledné eso v rukáve: tento úkon nemusíme robiť so všetkou vodou naraz.

Pre jednoduchosť si teraz označme teplotu \(\SI{100}{\celsius}\) ako \(T = 1\) a množstvo vody \(\SI{1}{\kilo\gram}\) ako množstvo veľkosti \(1\). Skúsme si destilovanú vodu (ďalej „voda“) rozdeliť na dve polovice, ktoré budeme postupne prikladať k sieťovej vode (ďalej „zásobník“).

Prvé priloženie vyústi v polovici vody a zásobníku teploty \(\frac{2}{3}\). Po priložení zvyšnej polovice, tá spolu so zásobníkom dosiahne teplotu \(\frac{4}{9}\). Spojením polovíc vody získame \(1\) vody teploty \(\frac{\frac{2}{3}+\frac{4}{9}}{2}=\frac{5}{9}\). To je znovu zlepšenie oproti predchádzajúcemu výsledku. Môžete si vyskúšať, že pri delení na tretiny vedie tento algoritmus znova k lepšiemu výsledku. Podobne pri štvrtinách, pätinách, …, \(n\)-tinách. Pozrime sa, aká bude výsledná teplota pre všeobecné delenie. Vezmime prvý kúsok veľkosti \(\frac{1}{n}\). Priložením k zásobníku ho dostaneme (spolu so zásobníkom) na teplotu \(\frac{1}{1+\frac{1}{n}}\). Toto rad za radom spravíme so všetkými \(n\) \(n\)-tinami.

Teplota každého kúsku po priložení bude vyzerať takto: \[ \frac{\textrm{pôvodná teplota kúsku} \cdot \textrm{veľkosť kúsku} + \textrm{aktuálna teplota zásobníka}\cdot\textrm{veľkosť zásobníka}}{\textrm{veľkosť kúsku a zásobníka dokopy}}\text{.} \]

Stačí si uvedomiť, že každým takým priložením klesne teplota zásobníka \(\frac{1}{1+\frac{1}{n}}\)-krát, a teda sme schopní žiadanú výslednú teplotu vody zapísať ako \[T_n=\frac{1}{n}\sum_{k=1}^{n} t_k=\frac{1}{n}\sum_{k=1}^{n} \left(\frac{1}{1+\frac{1}{n}}\right)^k\text{.}\]

Aj nepozorným okom sa dá v žiadanom súčte vypozorovať súčet geometrického radu. Pre ten, ako možno vieme platí \[ q+q^2+q^3+...+q^n = q\frac{1-q^n}{1-q}\text{,} \]

čo v našom prípade znamená, že \[ T_n = \frac{1}{n}\frac{1}{1+\frac{1}{n}}\frac{1-\frac{1}{\left(1+\frac{1}{n}\right)^n}}{1-\frac{1}{1+\frac{1}{n}}}=1-\frac{1}{\left(1+\frac{1}{n}\right)^n}\text{.} \]

Možno je čitateľovi známe, možno nie, že výraz \(\left(1+\frac{1}{n}\right)^n\) sa pri rastúcom \(n\), blíži (zdola) k číslu \(e\). Z tejto vedomosti vieme nahliadnuť, že zvyšovaním počtu kúsov vody sa vieme na hocako blízko priblížiť (zdola) k hodnote \[ T = 1-\frac{1}{e}\text{,} \] čo je síce znova viac, než sme mali predtým, avšak teplota povedzme \(\num{0.64}\) sa takýmto algoritmom dosiahnuť nedá.

Spomenieme si, že svoj výsledok sme práve zlepšili rozkúskovaním vody. Jediná vec, ktorú nám teraz ostáva vyskúšať, je rozkúskovať aj zásobník. Na začiatok rozdeľme vodu i zásobník na polovice. Postupne priložme polovicu vody k obom poloviciam zásobníka. Takto ju ohrejeme na \(\frac{3}{4}\), pričom nám zostali polovice zásobníka s teplotami \(\frac{1}{2}\) a \(\frac{3}{4}\). Teraz už s touto polovicou vody nevieme robiť nič, čo by zvýšilo jej teplotu.

Sústreďme svoju pozornosť na ešte nevyužitú polovicu vody. Nastáva dilema: ku ktorej polovici zásobníka ju priložiť ako prvej? Uvedomme si, že teplota polovice vody po priložení je polovica niečoho. Chceme čo najvyššiu teplotu, teda chceme čo najväčšie niečo. Zároveň aj niečo je súčtom voľačoho a polovice dačoho.

Spracovaním tohoto kúsku textu sa možno dopracovať k záveru, že chceme polovicu vody priložiť k teplejšej časti zásobníka ako poslednej, aby vo pri jej teplote vo výsledku stála \(\frac{1}{2}\) v čo najmenšej mocnine. Vykonáme teda prikladania v takomto rozumnom poradí a dostaneme sa k výslednej teplote celej vody \(\frac{5}{8}\). To je síce menej ako \(1-\frac{1}{e}\), avšak je to povážlivo blízko a vyžaduje to oveľa menej krokov.

Ak si však čitateľ skúsi aplikovať tento algoritmus pri delení vody i zásobníka na \(n=3\) častí, zistí, že hocako veľké delenie len vody bez delenia zásobníka sa môže schovať. Vyvstáva otázka, na akú teplotu vieme ohriať vodu ak použijeme náš svetoborný algoritmus na všeobecné \(n\). Pre istotu si ho ešte jasne napíšme:

1. Rozdeľme vodu i zásobník na \(n\) rovnakých častí.
2. Vezmime jednu časť vody a postupne ju priložme ku všetkým kúskom zásobníka.
3. Opakujeme rad za radom so zvyšnými časťami vody, pričom pri kúskoch zásobníkov postupujeme od tých s nižšou teplotou k tým s vyššou.
4. Zlejeme všetky kúsky vody dokopy.

Ekvivalentne:

1. Rozdeľme vodu i zásobník na \(n\) rovnakých častí.
2. Vezmime jednu časť zásobníka a postupne k nej priložme všetky kúsky vody.
3. Opakujeme rad za radom so zvyšnými časťami zásobníka.
4. Zlejeme všetky kúsky vody dokopy.

Ako na podnose sa nám ponúka napísať program, ktorý by nám týmto algoritmom vyprodukoval výslednú teplotu vody. Sklamúc ozajstných labužníkov sa touto cestou po autorovom súkromnom okúsení analytického prístupu i vydáme. Spíšeme, skompilujeme, spustíme, vykreslíme, vidíme:

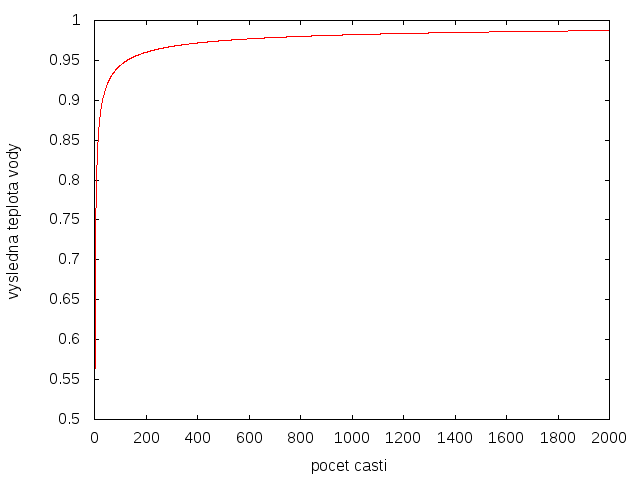
Tušíme, že zvyšovaním \(n\) sa možno s teplotou destilovanej vody dostať hocako blízko ku \(\SI{100}{\celsius}\), v čom sa dá nado všetku spoločensky štandardnú pochybnosť presvedčiť výpočtom výslednej teploty pre nejaké veľké \(n\).

V lepší výsledok sme ani nemohli dúfať, čo nás odbremeňuje od povinnosti dokázania, alebo aspoň naznačenia neprekonateľnosti nášho výsledku. Podstata výsledku nás však stavia do neľahkej situácie, na otázku zo zadania totiž nejestvuje odpoveď. Keďže s hocako veľkým, ale predsa konečným počtom kúskov sa vieme dostať hocako blízko, ale predsa nie úplne ku \(\SI{100}{\celsius}\), musíme puristicky odpovedať:

Najvyššia teplota, na ktorú vie Duško ohriať \(\SI{1}{\kilo\gram}\) destilovanej vody, neexistuje.

Napokon nedá nám nespomenúť, že podobné zariadenia pracujúce ale s plynmi napr. vo forme dvoch do seba vložených rúr, v ktorých prúdi plyn alebo kvapalina proti sebe, sa naozaj používajú v praxi na rekuperáciu tepla.