3. Fáro, ktoré slúži vzorové riešenie

Ujasnime si najprv, čo znamenajú niektoré mystické pojmy, ktoré sa vyskytli v zadaní. Napríklad taký výkon. Výkon je rýchlosť, akou je niečo schopné meniť energiu. Či už je to rýchlovarná kanvica, nohy cyklistu, alebo motor v aute, každá z týchto vecí má za úlohu premieňať energiu z jednej formy na druhú a práve rýchlosť, akou je to schopná robiť, sa nazýva výkonom. Povedané rečou istého čudáckeho spolku¹: \[ P=\frac{\Delta E}{\Delta t}\text{.} \qquad(1)\]

Odtiaľ vidíme, že jednotka výkonu bude \(\si{\joule\per\second}\), t. j. joule za sekundu, ako by sme očakávali. Táto jednotka sa volá Watt a stroj s výkonom 1 Watt je schopný dodať energiu 1 joule za jednu sekundu. V našej úlohe má motor s výkonom \(P = \SI{100}{\kilo\watt}\) urýchliť auto s hmotnosťou \(m = \SI{2000}{\kilo\gram}\) najprv z nuly na rýchlosť \(v_1 = \SI{100}{\kilo\metre\per\hour}\) a potom z \(v_1 = \SI{100}{\kilo\meter\per\hour}\) na \(v_2 = \SI{200}{\kilo\metre\per\hour}\).

Akým zmenám energie to zodpovedá? Keďže auto sa samozrejme pohybuje po ceste, ktorá je vo vákuovom tuneli a má dokonalé kolesá bez valivého odporu, jediná energia, ktorá tu bude hrať úlohu, je kinetická energia auta. Keby auto napríklad aj stúpalo do kopca, museli by sme zarátať aj gravitačnú potenciálnu energiu. Takže chudák motor musí v prvom prípade dodať² autu energiu \[ E_1=\frac{1}{2}mv_1^2 \]

a v druhom \[ E_2 = \frac{1}{2}mv_2^2-\frac{1}{2}mv_1^2\text{.} \]

A keď použijeme 1, dostaneme \[ t_1 = \frac{E_1}{P} = \frac{mv_1^2}{2P} \]

a \[ t_2 = \frac{E_2}{P} = \frac{mv_2^2-mv_1^2}{2P}\text{.} \]

Pozrime sa teraz na čas. Máme za úlohu zistiť, koľko bude trvať autu idúcemu na plný výkon, kým prejde vzdialenosť \(\SI{1}{\kilo\metre}\). Musíme teda nájsť závislosť prejdenej dráhy na čase. Z prvej časti úlohy vieme závislosť rýchlosti na čase: \[ v = \sqrt{\frac{2Pt}{m}}\text{.} \]

Ako z tohoto získame závislosť prejdenej dráhy na čase? Ak by sme mali rýchlosť konštantnú, mohli by sme použiť jednoduchý vzorec \(s=vt\). Ale nemáme. Alebo máme? Skúsme si uvedomiť, čo to vlastne \(vt\) znamená. Ak by sme mali graf rýchlosti v závislosti od času, konštantná rýchlosť by tam predstavovala len rovnú čiaru, ktorá by neklesala ani nestúpala:

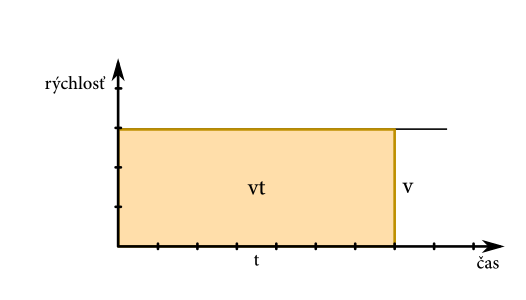
Vidíme, že vzorec \(vt\) tu predstavuje iba plochu obdĺžnika, ktorého jedna strana je \(v\) a druhá strana je \(t\). Takže máme zaujímavý výsledok: dráha prejdená počas pohybu s konštantnou rýchlosťou je rovná ploche ohraničenej grafom rýchlosti v závislosti na čase. Funguje tento princíp aj pre iné prípady? Napríklad rovnomerne zrýchlený pohyb. Vtedy rýchlosť stúpa z časom rovnomerne: \[ v=at\text{.} \]

To znamenám že grafom rýchlosti bude priamka, ktorej smernica (strmosť) závisí od zrýchlenia. Pozrime sa teda:

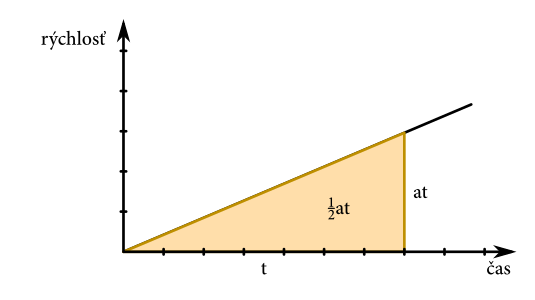
vidíme, že tentoraz bude plocha pod grafom pravouhlý trojuholník, s jednou stranou \(t\) a druhou \(at\). Plocha medzi časom \(0\) a časom \(t\) je teda \[ s=\frac{1}{2}at^2\text{.} \]

A tu môžete naozaj spoznať dráhu pre rovnomerne zrýchlený pohyb. Zdá sa, že náš objav platí aj pre tento prípad. Prečo by nemal platiť aj pre prípad, že grafom bude napríklad odmocnina? Na zistenie prejdenej dráhy teda stačí nájsť plochu pod grafom funkcie. Ale ako to urobíme, keď funkcia nemá nejaký pekný tvar, ako napríklad priamka? Mohli by sme napríklad graf nakresliť na papier, vystrihnúť a potom odvážiť a z plošnej hustoty papiera by sme určili plochu.

My ale vyriešme tento problém bez toho, aby sme sa vôbec museli postaviť od stola! To znamená: naprogramujme ho! Ak ste ešte nikdy neprogramovali, nemusíte sa báť, programovať budeme len v tzv. tabuľkovom procesore. A také programovanie je ľahké, lebo skoro všetko za vás urobí samotný tabuľkový procesor. Tabuľkový procesor je taká vec ako napríklad Excel alebo OpenOffice Calc, kde môžete do tabuliek vkladať svoje hodnoty a potom s nimi nejako počítať. A čo je pre nás najdôležitejšie, tieto programy vedia mnoho vecí automatizovať a mnoho vecí si vedia sami domyslieť. Môžeme ich teda využiť na vykonanie ohromného množstva výpočtov vo veľmi krátkom čase.

Tak dosť bolo táranín, poďme už na samotný výpočet. Plochu akého útvaru vieme určiť najjednoduchšie? Predsa obdĺžnika. Tak prečo nerozložiť našu odmocninovú plochu na obdĺžniky? Určite si teraz hovoríte: „Čo je to za hlúpy nápad! Veď odmocninová plocha je oblá! Ako ju chce rozložiť na obdĺžniky?“

No dobre. A čo keď urobíme tie obdĺžniky také úzke, že už skoro ani nebude vidno, že sú to obdĺžniky? Ak rozložíme nejakú plochu na \(\num{100000}\) obdĺžnikov, môžete sa staviť, že rozdiel medzi ich spoločnou plochou a skutočnou oblou plochou bude zanedbateľný. Ak by ste plochu \(\num{100000}\) obdĺžnikov chceli počítať ručne, môžete si rovno ustlať na cintoríne. Ale predsa sme spomínali nejaké tie počítače. Nakopnite teda tie turbo mašiny HP-čko Intel Pentium 100 MHz z deväťdesiateho druhého a stále to budete mať \(10^{18}\)-krát rýchlejšie ako s ceruzkou a papierom. Takže, toto je schéma výpočtu:

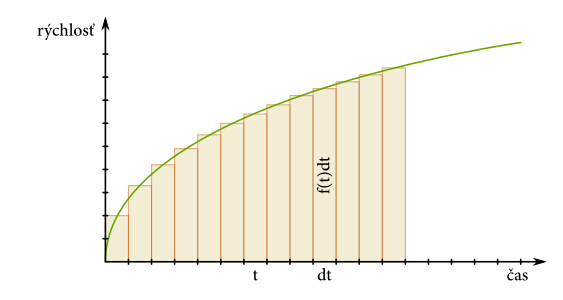
Ak budú obdĺžniky naozaj úzke, pokryjú úplne celú plochu. V našom výpočte bude mať každý obdĺžnik šírku \(\num{0.001}\). Výška obdĺžnika, ktorý sa nachádza na časovej súradnici \(t\) je \(f(t)\) a jeho plocha bude teda \(\num{0.001} \cdot f(t)\). A už zostane len plochy všetkých obdĺžnikov sčítať. Postup je jasný, ostava ho už iba implementovať. Vzhľadom na náročnosť výpočtu, my sme použili tabulkový procesor (Excel), ale je v podstate jedno ako to urobite.

Teraz prichádza moment, na ktorý by ste nemali po vyriešení úlohy nikdy zabudnúť. A tým je zamyslenie sa. Je 28 sekúnd na jeden kilometer zmysluplná hodnota? Dala by sa dosiahnuť bežným autom, alebo na to treba Formulu 1? Alebo je to slimačie tempo?. To pri rýchlosti ktorá má priebeh odmocniny ťažko posúdite, ale jednu vec môžeme predsa len otestovať.

Ak si predstavíme, že auto malo po celú dobu konštantné zrýchlenie a použijeme vzorec pre rovnomerne zrýchlený pohyb, to, čo dostaneme, bude priemerné zrýchlenie. A keďže priemerné zrýchlenie je také, že auto v skutočnosti zrýchľovalo chvíľku viac a chvíľku menej, tak ak by náhodou už priemerné zrýchlenie bolo nezmyselne vysoké alebo nízke, vedeli by sme, že je zle. Môžete si overiť, že v tomto prípade je priemerné zrýchlenie asi \(\SI{2.5}{\metre\per\second\squared}\), čo sa zdá byť celkom normálne.

Aby sme uspokojili nenásytnosť zadávateľa úlohy, ostávajú už len grafy. Pre polohu použijeme hodnoty, ktoré sme si numericky vypočítali, pre rýchlosť máme vzorec. Ostáva ešte zrýchlenie – na to použijeme vzorec \[ P = Fv\text{,} \]

čo je len základný vzťah pre prácu predelený časom. Keďže \(F=ma\) a rýchlosť poznáme, môžeme si vyjadriť \[ a = \sqrt{\frac{P}{2mt}}\text{.} \]

Rýchlosť a zrýchlenie máme teda vyjadrené ako funkcie, ktoré si môžeme dať vykresliť a graf polohy urobíme v Exceli. Uf!

Ešte poznámka na záver

To čo sme robili v tabuľkovom procesore, teda sčítavanie plochy pod grafom, sa volá integrovanie. My sme to robili numericky, to znamená vykonaním veľkého množstva jednoduchých výpočtov hrubou silou. Ale dá sa to aj analyticky – to znamená, že na to existuje matematická procedúra, ktorou sa dá plocha pod grafom vypočítať len s použitím rozumu a v priebehu niekoľkých sekúnd. Ako sa to robí sa dozviete, keď prídete študovať sem k nám na Matfyz (alebo keď budete mať šťastie, už na strednej škole :)). Ak už náhodou integrovať viete, určite vyriešte túto úlohu aj tým spôsobom.

Pridávam tu ešte aj kratučký program na numerické itegrovanie v C++. Určite sa na to pozrite, aj keď neviete programovať. Programovanie je z veľkej časti intuitívna záležitosť. Ak si dobre premyslíte, čo vlastne od počítača chcete, v skutočnosti sa nemusíte na programovanie nič „učiť“, maximálne tak technické záležitosti – kde dať bodkočiarku alebo zloženú zátvorku alebo ako sa volá ten príkaz, atď…