2. My, Jara strativší vzorové riešenie

Zadanie

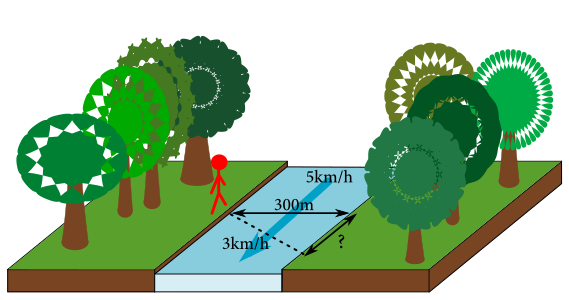
Vášnivý geograf Jaro má doma kopu máp z rôznych kútov sveta, rôzne starých. Občas si nejakú z nich vezme so sebou na turistiku. Minule sa dostal do prekérnej situácie. Potreboval sa dostať cez rieku a na mape cez ňu našiel most, tak sa k nemu vydal. Keď však prišiel na miesto, zistil, že most tam z nejakých dôvodov nie je. Vždy pripravený Jaro teda vytiahol plavky a skúmavým okom si premeral rieku. Zamyslel sa:

„Rieka je široká \(\SI{300}{\metre}\) a tečie rýchlosťou \(\SI[per-mode = symbol]{5}{\kilo\metre\per\hour}\). Viem plávať rýchlosťou \(\SI[per-mode = symbol]{3}{\kilo\metre\per\hour}\). Ako najbližšie k miestu, ktoré je priamo oproti mne, viem doplávať?“

Pomôžete mu v tejto ťažkej situácii?

Ako uchopiť tento problém? Ukážeme si dve riešenia, jedno pekné geometrické a druhé matematické a konceptuálnejšie náročnejšie.

Geometrické riešenie

Celý problém, ktorý je potrebné vyriešiť, je pretransformovať rýchlosť Jara zadanú vzhľadom na rieku do sústavy spojenej so Zemou.

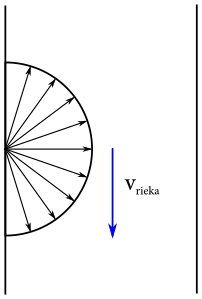
Jaro sa vzhľadom na vzťažnú sústavu rieky môže vybrať všetkými smermi od \(0\) po \(2 \pi\). Konce všetkých možných vektorov jeho rýchlosti tvoria kružnicu. Čo sa stane, ak ku týmto vektorom pripočítame vektor \(v_r\)? Je to ekvivalentné transformácii riečnej vzťažnej sústavy na pohyb vzhľadom na breh. Ku každému z pôvodných Jarových rýchlostných vektorov musíme pripočítať rýchlostný vektor rieky. Ako budú teraz vyzerať konce všetkých takto posunutých vektorov? Stále budú tvoriť kružnicu, ale jej stred bude posunutý o vektor \(v_r\).

Z našich nových vektorov musíme vybrať ten, ktorý ukazuje najbližšie k vytúženému bodu na druhom brehu. Nuž a to je dotyčnica k tejto posunutej kružnici.

Vidíme, že uhol \(\phi\) výsledného pohybu vieme určiť ako \[ \phi = \arccos\left(\frac{3}{5}\right)\text{.} \]

Pokiaľ pod týmto uhlom prejdeme \(x\)-ovú vzdialenosť \(L=\SI{0.3}{\kilo\metre}\), vzdialenosť \(y\) určíme ako \[ h = L \tan{\left(\arccos\left(\frac{3}{5}\right)\right)}\text{.} \]

Ak sme si za nulu zvolili bod, kde stojí Jaroslav, platí \(y =-h\).

Výsledok je \(y=\SI{-0.4}{\kilo\metre}\). Na domácu úlohu si premyslite, prečo stačí uvažovať iba pohyb po úsečkách. Mínus vo výsledku odzrkadľuje fakt, že smer osi \(y\) sme zvolili v opačnom smere, ako tečie rieka.

Analytické riešenie

Teraz si ukážeme analytické riešenie, v ktorom prídeme k funkcii vzdialenosti a nájdeme jej minimum pomocou derivácie. Pokiaľ vás predchádzajúca veta vydesila, pokojne preskočte druhú polovicu vzoráku.

Zavedieme súradnicovú sústavu. Ako to už vo fyzike býva, dobrá voľba súradnicovej sústavy je polovica úspechu. Os \(y\) zvolíme tak, aby kladný smer bol orientovaný proti smeru toku rieky.

Potom jej rýchlosť je \[ \vec{v_r} = \begin{bmatrix} 0 \\ 5 \end{bmatrix} \si{\kilo\metre\per\second}\text{.} \]

Jaro je schopný plávať rýchlosťou \(v_0 = \SI{3}{\metre\per\second}\) vzhľadom na vzťažnú sústavu rieky. Poznáme veľkosť jeho rýchlosti. Pokiaľ pláva pod uhlom \(\phi\) od brehu, vektor jeho rýchlosti je \[ \vec{v_J} = \begin{bmatrix} v_{0} \sin\phi \\ v_{0} \cos\phi \end{bmatrix}\text{,} \]

Nulový uhol stotožníme so stavom, kedy obe rýchlosti majú ten istý smer. Výsledná rýchlosť Jara vzhľadom na breh je \[ \vec{v} = \vec{v_J} + \vec{v_r} \begin{bmatrix} v_{0} \sin\phi \\ v_{0} \cos\phi - 5 \end{bmatrix}\text{.} \]

Aby sa Jaro dostal na druhý breh, musí preplávať vzdialenosť \(L=\SI{0.3}{\kilo\metre}\) v \(x\)-ovom smere. Čas, za ktorý sa tam dostane, je \[ t = \frac{L}{v_x} = \frac{L}{v_{0} \sin\phi}\text{.} \]

Zatiaľ sa v \(y\)-ovom smere posunie o \[ y = v_y t = L \frac{v_0 \cos\phi - 5}{v_{0} \sin\phi} = \frac{3 \cos\phi - 5}{10 \sin\phi}\text{.} \]

Nás zaujíma, akú najmenšiu hodnotu môže \(y\) dosiahnuť. Čiže hľadáme minimum funkcie \(y(x)\). Buď pomocou Wolfram|Alpha¹ si vykreslíme graf a určíme minimum, alebo derivovaním zistíme, že minimum je pri polohe \[ y = \SI{-0.4}{\kilo\metre}\text{,} \]

Využili sme pritom matematickú znalosť, ktorá hovorí, že v bode, kde funkcia dosahuje svoju minimálnu alebo maximálnu hodnotu, je derivácia nulová: \[ \frac{\mathrm{d}y(x)}{\mathrm{d}x} \overset{!}{=} 0\text{,} \]

odkiaľ \[ x = 2 \arctan\frac{1}{2}\text{.} \]

Takže sme si ukázali názorný algoritmický postup. Nemusíte sa trápiť, ak ešte neviete, čo je derivácia. Stačí, ak si zapamätáte, že sa pomocou nej dá nájsť extrém funkcie a že so samotným výpočtom vám dokáže pomôcť počítač.