4. GPS vzorové riešenie

Na začiatok si stručne zopakujme, čo sú vlastne tie GPS súradnice, ktorými určujeme polohu. Prvá súradnica, zemepisná šírka, je uhol medzi rovinou rovníka a spojnicou stredu Zeme s miestom, ktorého súradnice určujeme. Rovník má teda \(\ang{0}\) zemepisnej šírky, severný pól \(\ang{90}\) a južný pól \(\ang{-90}\). Druhou súradnicou je zemepisná dĺžka, teda uhol, ktorý zviera rovina miestneho poludníka s nultým (greenwichským) poludníkom, pričom poludník je polkružnica spájajúca severný pól s južným. Zemepisná šírka sa teda udáva v stupňoch od \(\ang{180}\) západnej zemepisnej dĺžky po \(\ang{180}\) východnej zemepisnej dĺžky.

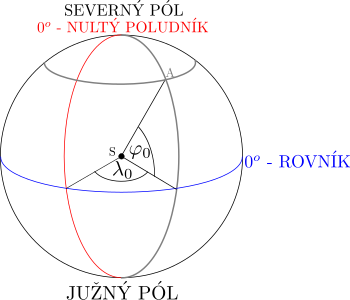
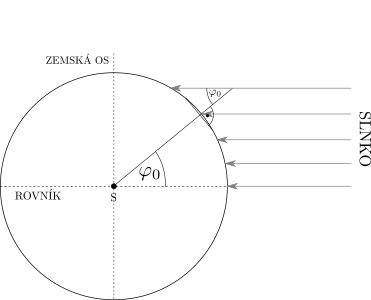
Ako však zistiť tieto súradnice bez použitia mapy? Začnime zemepisnou šírkou. Tu existujú dve možnosti. Môžeme merať buď na pravé poludnie¹ pomocou Slnka alebo v noci za použitia Polárky. Princíp je v tom, že Slnko (alebo Polárka) je voči Zemi ako objektu umiestnené v konkrétnom smere (viď obr. ?? pre Slnko a obr. ?? pre Polárku). Avšak nakoľko Zem nie je rovina, ale v podstate guľa², uhol, pod ktorým vidíme Slnko (alebo Polárku), sa môže líšiť. Nuž a presne na pravé poludnie v deň jarnej alebo jesennej rovnodennosti³, je \(\ang{180}\), mínus uhol medzi Slnkom a kolmicou k zemi⁴ rovný presne zemepisnej šírke (viď obr. ??).

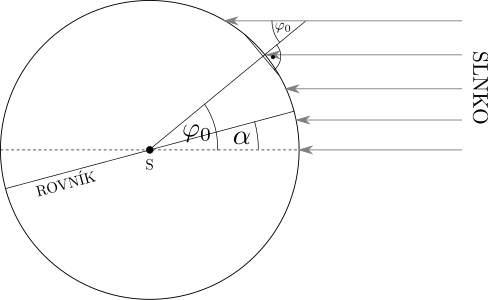
Samozrejme, zemepisnú šírku vieme merať aj v iný deň. Vtedy je však potrebné odpočítať deklináciu Slnka⁵ (viď obr. ??).

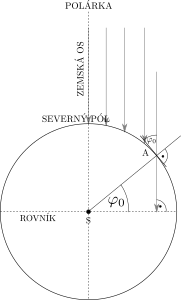
S Polárkou je meranie jednoduchšie v tom, že sa nachádza presne nad zemskou osou a teda jej poloha sa na oblohe nemení – takže kým vidíme hviezdy (a hlavne Polárku), môžeme merať kedykoľvek. V tomto prípade uhol vodorovného smeru a smeru k Polárke predstavuje práve zemepisnú šírku:

Princíp merania zemepisnej dĺžky je o niečo jednoduchší.⁶ Spočíva v tom, že Zem sa otáča konštantnou rýchlosťou \(\ang{360}\) za 24 hodín (prepočítajme na niečo výhodnejšie: \(\ang{1}\) za 4 minúty). Ak teda vieme určiť, kedy je u nás presné poludnie a kedy bolo pravé poludnie na nultom poludníku, z ich rozdielu už vieme zemepisnú dĺžku jednoducho určiť – je to spomínaný rozdiel časov delený 4 (dostaneme teda počet stupňov, o ktorý sa Zem medzičasom otočí, čo je vlastne presne to, čo sme chceli :)). Už chýba len určiť smer. Ak je u nás viac hodín než v Greenwichi⁷, u nás bolo poludnie skôr a teda sme východnejšie alebo naopak, ak by u nás bolo menej hodín, poludnie by bolo skôr na Greenwichi a zisťovaná súradnica by bola západnej zemepisnej dĺžky.

Meranie

K meraniu je potrebné vyriešiť ešte dve otázky. Prvou je: ako zistiť, kedy je pravé poludnie? Druhou: ako odmerať daný uhol? V prípade zemepisnej dĺžky sme nájdením odpovede na prvú otázku vlastne už vyhrali, zatiaľ čo pri zemepisnej šírke potrebujeme hlavne odpoveď na tú druhú. Čas pravého poludnia vieme určiť buď pomocou faktu, že tieň ukazuje presne na skutočný sever⁸ – rovník je na juh od nás a Slnko vtedy nie je ani na východe, ani na západe – alebo využitím skutočnosti, že tieň je vtedy najkratší (Slnko je predsa v najvyššom bode svojej dráhy). Ďalšou možnosťou je merať uhol k Slnku a poludnie by bolo vtedy, keď je uhol maximálny. Na Greenwichi však poludnie nie je presne 12:00 (alebo 13:00 letného času)⁹. Kedy bolo alebo bude, viete vyčítať napríklad z tejto tabuľky: http://www.ppowers.com/EoT.htm/

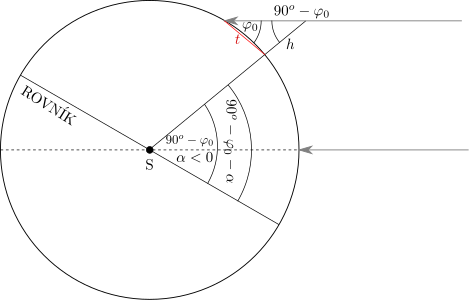
Čo sa týka odpovede na druhú otázku, prvou možnosťou je odmerať výšku \(h\) nejakého predmetu, na ktorý cez poludnie svieti Slnko. V tom prípade je taktiež potrebné zistiť dĺžku jeho tieňa \(t\) na pravé poludnie. Potom z uvedených údajov je možné vypočítať zemepisnú šírku \(\phi\) použitím vzťahu jasného z obr. ??: \[ \phi = \ang{90} - \arctan{\left(\frac{h}{t}\right)} - \alpha\text{,} \qquad(1)\] kde \(\alpha\) je deklinácia Slnka.

Ďalším možným spôsobom je vytvoriť si na to špeciálny uhlomer. Ja som zvolila nasledujúci model: dve dosky pribité klincom tak, že jednu položíme kolmo na zem a druhou môžeme spokojne otáčať. Na klinec taktiež zavesíme závažie, aby sa ľahšie a presnejšie odčítaval uhol.

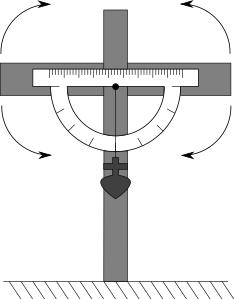
Keď je rotačná časť vodorovne, uhlomer ukazuje presne \(\ang{90}\) (prípadne inú konštantu, ak lepíte krivo). Následne využitím tieňa – tieň rotačnej časti má minimálny obsah práve vtedy, keď ňou mierime priamo na Slnko¹⁰ – zistíme, akému uhlu zodpovedá smer k Slnku a nakoniec už len rozdielom uhlov a prípadným odčítaním deklinácie Slnka, ktorú pre daný deň nájdeme v deklinačnej tabuľke¹¹ určíme hľadanú zemepisnú šírku.

Ak by sme sa rozhodli merať v noci, pre mierenie na Polárku by bolo ideálne použiť dobrý laser. Laser priložíme k rotačnej časti a namierime tak, aby svietil na Polárku. Nakoniec už len určíme hľadaný uhol a máme vyhraté. Ja som bohužiaľ laser nemala, tak som rotačnú časť namierila rovnobežne s mojou rukou ukazujúcou na Polárku a na moje prekvapenie bol výslený uhol odlišný len o \(\ang{1}\) (\(\ang{49}\) miesto \(\ang{48.185}\))¹² Ten jeden stupeň je v skutočnosti dosť značný rozdiel. Ak vás však zaujíma len približné miesto na Zemi, kde sa nachádzate, tak je tento spôsob v poriadku. Pri navigácií na mori by ste sa však dlho asi nedožili.

Hlavnú pozornosť merania som však sústredila na poludnie. Pomocou uhlomerovo-tieňovej metódy som namerala uhol medzi kolmicou a smerom k Slnku: \(\ang{51}\). Deklinácia Slnka v daný deň bola \(\ang{-2.6}\), takže zemepisná šírka by mala byť rovná \(\ang{53.6}\). To je však takmer až o \(\ang{6}\) zle (správna hodnota: \(\ang{48.185}\) N). Druhý spôsob, ktorý som zvolila, bolo vytvorenie slnečných hodín. Na veľký kus kartónu som nalepila ceruzku, ktorej výšku som si zmerala, a v okolí obeda som si každú minútu značila polohu tieňa. Pri prvej realizácii, keď deklinácia Slnka bola \(\ang{-1.8}\) a poludnie na nultom poludníku 12:51 GMT, mi poludnie u nás vyšlo 12:53 – zemepisná dĺžka rovná 58/4 = \(\ang{14.5}\) (miesto skutočných \(\ang{17.071}\)) – a zemepisná šírka podľa rov. 1: \(\ang{50.5}\) N.

Čiže namiesto skutočnej lokácie v Bratislave mi vyšlo, že sa nachádzam kúsok severne od Prahy. Druhé opakovanie merania bolo s deklináciou \(\ang{-2.6}\) a poludním na nultom poludníku 12:50 (ten istý deň, čo uhlomer-tieňové meranie). Poludnie mi vyšlo o 12:46, z čoho vychádza zemepisná dĺžka \(\ang{16}\)E a zemepisná šírka (zo vzťahu 1) \(\ang{52.9}\) – čo je však už takmer severná časť Poľska. Hlavným problémom v daný deň bolo časté prechádzanie oblakov popred slnko a tým pádom žiaden tieň – nebolo možné spozorovať každú minútu. Nepresnosti mohli byť aj v určovaní dĺžky tieňa. Veľmi užitočnou pomocou pri meraní je kamarát, ktorý vám pomôže uchycovať predmety vodorovne/kolmo – pravdepodobne jeden z výrazných faktorov, prečo mi nočné meranie vyšlo o toľko presnejšie. Vyhovujúce by bolo zvoliť aj vhodné závažie, ktoré sa ľahko popasuje s vetrom.