6. Vladkove kvetináče vzorové riešenie

Pri riešení tejto úlohy budeme vychádzať z Bernoulliho rovnice v tvare \[\frac{P}{\rho} + \frac{1}{2}v^{2}+gh = \text{konštanta.}\]

Môžeme uvažovať, že rozdiel atmosférických tlakov je zanedbateľný a vyjadríme si \(v_{1}\) z rovnice kontinuity, \[vS = \text{konštanta.}\]

Toto dosadíme naspäť do Bernoulliho rovnice a vyjadríme z nej \(v_{2}\) \[gh=\frac{1}{2}v_{2}^{2}\left(1-\frac{S_{2}^{2}}{S_{1}^{2}}\right)\text{,}\] \[v_{2} = \sqrt{ \frac{2gh}{1 - \frac{r_{2}^{4}}{r_{1}^{4}}} }\text{.}\]

Polomer kvetináča je oveľa väčší než polomer dierky, takže zložku obsahujúcu \(v_{1}\) zanedbáme a dostávame \(v_{2}=\sqrt{2gh}\). Zo vzťahu pre \(v_{2}\) už vieme zbadať, že voda bude z kužeľa vytekať priemerne väčšou rýchlosťou ako z valca, keďže zrezaný kužeľ má viac objemu v hornej polovici, no stále ešte nevieme, za aký čas budú prázdne. Potrebný čas zrátame pomocou nejakého výpočtového programu.

Venujme sa najprv valcu. Zapíšme rozmery kvetináča, teda polomer/priemer kvetináča, výšku vodnej hladiny a polomer dierky, ktorou voda vyteká. Stanovme si nejaké \(\mathrm{d}t\), ktorým označíme krátky časový úsek. Vytvorme cyklus, pomocou ktorého zistíme výšku v čase \(t+\mathrm{d}t\). Z \(h(t)\) poznáme \(v(t)=\sqrt{2gh(t)}\), z ktorého vyrátame \(\mathrm{d}V\), označujúce objem, ktorý vytečie z nádoby od \(t\) po \(t+\mathrm{d}t\). Získavame \(\mathrm{d}V(t)=v(t)S_{d}\mathrm{d}t\), kde \(S_{d}\) je plocha dierky. Z vytečeného objemu následne zrátame výšku hladiny v \(t+\mathrm{d}t\) \[h(t+\mathrm{d}t)=h(t)-\frac{\mathrm{d}V(t)}{S_{p}}\text{.}\]

Riešime analogicky pre zrezaný kužeľ až po \(\mathrm{d}V(t)\). Pokles bude rozdielny, keďže s výškou hladiny sa mení aj jej polomer. Vypočítame ho z podobnosti trojuholníkov. Označme si \(x\) výšku nezrezanej časti kužeľa, potom platí \[\frac{r(t)}{h(t)+x}=\frac{r_{p}}{x}=\frac{r(0)}{h(0)+x}\text{.}\]

Vyjadríme \(x\): \[x=\frac{r_{p}h(0)}{r(0)-r_{p}}\text{.}\]

A následne \(r(t)\): \[r(t)=\frac{h(t)}{h(0)}(r(0)-r_{p})+r_{p}\text{.}\]

Z \(r(t)\) vypočítame \(S(t)\), ktoré dosadíme do \[h(t+\mathrm{d}t)=h(t)-\frac{\mathrm{d}V(t)}{S(t)}\text{.}\]

Už len zadáme vzorce do tabuľkového procesora a potiahneme tabuľky dole, až dostaneme \(h(t) \leq 0\) alebo napríklad v Pythone do while (h > 0) funkcie, ktorá zráta, kedy všetka voda vytečie. Úlohu sme teda vyriešili a môžeme vytvoriť grafy z vypočítaných údajov.

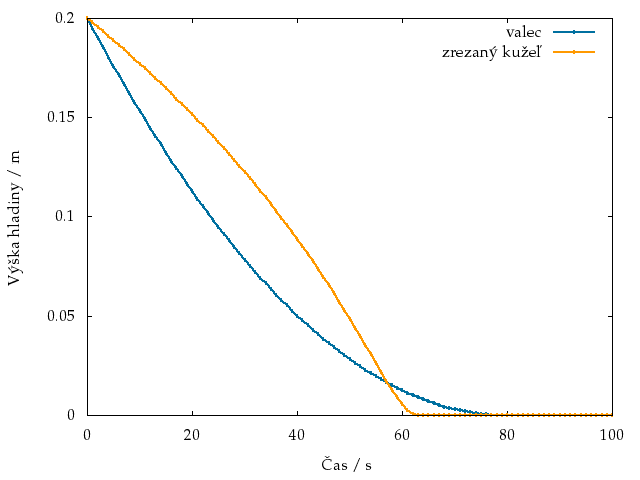
Modrou je na grafe označený valcový kvetináč (\(r_{p} = \SI{0.1}{\metre}\), \(r_{d} = \SI{0.005}{\metre}\), \(h(0) = \SI{0.2}{\metre}\), \(\mathrm{d}t = \SI{1}{\second}\)), ktorý vytečie približne za 78 sekúnd a oranžovou kvetináč v tvare zrezaného kužeľa (\(r(0) = \SI{0.15}{\metre}\), \(r_{p} = \SI{0.05}{\metre}\), \(r_{d} = \SI{0.005}{\metre}\), \(h(0) = \SI{0.2}{\metre}\), \(\mathrm{d}t = \SI{1}{\second}\)), ktorý vytečie za 63 sekúnd. Vidíme, že aj keď je v kužeľovom kvetináči dlhodobejšie hladina vyššie, tak hladina vody vo valci klesá časom pomalšie a hladina vody v zrezanom kužeľi rýchlejšie, až v 57. sekunde bude vyššia hladina pre zmenu vo valci.

Programy v Exceli a v Pythone sa nachádzajú tu.