6. Rozladené kyvadlo vzorové riešenie

Zadanie

Slečna Noetherová¹ si zaobstarala nádherné dokonale symetrické rovinné matematické kyvadlo dĺžky \(l\), ktoré umiestnila medzi dve vertikálne sklenené dosky, aby mohla overovať symetrie časopriestoru. Na to však musí vedieť merať čas, a na to jej poslúži kyvadlo.

Nebol by v tom čert, teda presnejšie bol, keby za rohom nestál pán Heisenberg², ktorý zaryte tvrdí, že „Pravá krása je skrytá v asymetriách!“. Preto sa rozhodol, že bod závesu kyvadla aj s dvomi vertikálnymi sklenennými doskami³ nechá rotovať uhlovou rýchlosťou \(\Omega\).

Celé rovinné matematické kyvadlo teraz rotuje okolo osi prechádzajúcej bodom závesu ležiacej v rovine kyvadla (pozri obrázok). Vďaka tejto skutočnosti sa kyvadlo začne oneskorovať. Za aký najkratší čas sa kyvadlo oneskorí o pol periódy?

---

1. Pre tých, čo neboli na poslednom zimnom sústredení, naše zlatíčko Pľyš.↩

2. Maťo↩

3. Kyvadlo sa tak teda môže hýbať len v tenkej medzere medzi doskami, ktoré rotujú spolu s kyvadlom.↩

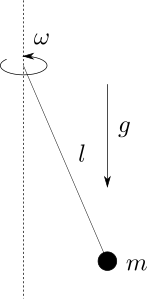
Takže poďme na to! Ako prvé si musíme vyjasniť, prečo by sa vôbec malo rotujúce kyvadlo oneskorovať. Pozrime sa naň vo vzťažnej sústave spojenej so sklenenými doskami, takže trajektórie oboch kyvadiel vyzerajú navlas rovnako, akurát časový priebeh polohy závažia kyvadla na tejto trajektórii je v jednotlivých prípadoch odlišný. V čom sa rotujúce kyvadlo líši od obyčajného? V ničom… lenže ho popisujeme v neinerciálnej vzťažnej sústave, preto naň pôsobí okrem tiažovej i neinerciálna odstredivá sila. Pozrime sa, ako sa to prejaví na pohybe kyvadla.

Aby sme mali referenčné výsledky, popíšme v krátkosti správanie nerotujúceho kyvadla. Podrobnú analýzu tu nebudeme robiť, pretože predpokladáme, že problematika obyčajného matematického kyvadla je všeobecne známa.¹ Po vychýlení kyvadla z rovnovážnej polohy naň pôsobí tiažová sila nenulovým momentom, ktorý sa ho snaží vrátiť do rovnovážnej polohy. V priblížení malých výchyliek koná kyvadlo harmonický pohyb s uhlovou frekvenciou \(\omega_{0}=\sqrt{g/l}\), a teda perióda obyčajného matematického kyvadla je \[ T_{0}=2\pi\sqrt{\frac{l}{g}}\text{.} \]

Teraz môžeme pristúpiť k analýze rotujúceho kyvadla. Budeme vychádzať z druhej vety impulzovej, ktorá hovorí, že časová zmena momentu hybnosti je rovná celkovému pôsobiacemu momentu síl.² Matematicky vyjadrené \[ \frac{\Delta\vec{L}}{\Delta t}=\vec{M}\text{.} \]

V zmysle analógie s translačným pohybom³ \(\left|\frac{\Delta\vec{L}}{\Delta t}\right|=J\epsilon\). Nech je kyvadlo vychýlené o uhol \(\phi\) z rovnovážnej polohy, napríklad v kladnom zmysle. Potom naň pôsobí tiažová sila momentom veľkosti \[ \left|\vec{M_G}\right|=\left|\vec{r_G}\times\vec{F_G}\right|=r_{G\bot}mg=mgl\sin\phi\text{.} \]

Priradíme mu znamienko „-“, pretože sa snaží vrátiť kyvadlo do rovnovážnej polohy, t. j. pôsobí v zápornom zmysle. Toto zatiaľ platí aj pre nerotujúce kyvadlo. Lenže v prípade rotácie roviny kmitania uhlovou rýchlosťou \(\Omega\) pôsobí aj odstredivá sila svojím momentom veľkosti \[ \left|\vec{M_o}\right|=\left|\vec{r_o}\times\vec{F_o}\right|=r_{o\bot}\cdot m\Omega^{2}\rho=l\cos\phi\cdot m\Omega^{2}l\sin\phi=\frac{1}{2}ml^{2}\Omega^{2}\sin\left(2\phi\right)\text{.} \]

Odstredivá sila „odtláča“ kyvadlo od rovnovážnej polohy, t. j. jej moment pôsobí v kladnom zmysle, preto mu priradíme znamienko „+“. Moment ťahovej sily lanka je nulový. Teraz už môžeme sformulovať pohybovú rovnicu rotujúceho matematického kyvadla \[ J\epsilon=-mgl\sin\phi+\frac{1}{2}ml^{2}\Omega^{2}\sin\left(2\phi\right)\text{.} \]

V priblížení malých uhlov platí \(\sin x\approx x\). Matematické kyvadlo predstavuje hmotný bod na nehmotnom závese, preto \(J=ml^{2}\). Aplikovaním týchto vzťahov dostávame \[ \epsilon+\left(\frac{g}{l}-\Omega^{2}\right)\phi=0\text{.} \]

Za predpokladu, že \(g>l\Omega^{2}\), v tom spoznávame rovnicu harmonického oscilátora s uhlovou frekvenciou \(\omega=\sqrt{g/l-\Omega^{2}}\). Perióda kmitania rotujúceho matematického kyvadla je teda \[ T=2\pi\sqrt{\frac{l}{g-l\Omega^{2}}}>T_{0}\text{.} \]

Zadanie sa nás pýta na čas \(\tau\), za ktorý sa rotujúce kyvadlo oneskorí o polperiódu oproti obyčajnému matematickému kyvadlu. Znamená to, že za tento čas rotujúce kyvadlo prekmitne \(n\)-krát, teda \(\tau=nT\), zatiaľ čo obyčajné kyvadlo prekmitne \(\left(n+\frac{1}{2}\right)\)-krát, čiže \(\tau=\left(n+\frac{1}{2}\right)T_{0}\). Dajme tieto vyjadrenia do rovnosti a dosaďme periódy. Jednoduchými matematickými úpravami dostaneme: \[ 2\pi n\sqrt{\frac{l}{g-l\Omega^{2}}}\overset{!}{=}2\pi \left(n+\frac{1}{2}\right)\sqrt{\frac{l}{g}} \] \[ n^{2}-\frac{g-l\Omega^{2}}{l\Omega^{2}}n-\frac{g-l\Omega^{2}}{4l\Omega^{2}}=0 \] \[ n=\frac{\sqrt{g-l\Omega^{2}}}{2l\Omega^{2}}\left(\sqrt{g-l\Omega^{2}}\pm\sqrt{g}\right) \]

Z vyjadrenia \(n\) v tomto tvare vidíme, že kladný počet prekmitnutí dostaneme pre „+“, čomu zodpovedá čas \[ \tau=nT=\frac{\pi}{\Omega^{2}}\left(\sqrt{\frac{g}{l}-\Omega^{2}}+\sqrt{\frac{g}{l}}\right)\text{.} \]

Poznámka pre náročných

V tomto momente sme sa dopracovali k výsledku, takže môžeme byť spokojní. Alebo žeby nie? V priebehu výpočtu sme narazili na situáciu, v ktorej sme predpokladali, že \(g>l\Omega^{2}\).

Čo by sa ale stalo, keby kyvadlo rotovalo tak rýchlo, že by táto podmienka nebola splnená? V takom prípade by riešenie pohybovej rovnice kyvadla neviedlo na harmonické kmity, ale na exponenciálny nárast výchylky. Znamená to, že by kyvadlo začalo šialene rotovať? Nie, pretože nami odvodená linearizovaná pohybová rovnica platí len pre malé výchylky.

Tak čo sa teda deje v prípade vysokej uhlovej rýchlosti otáčania? Aby sme to vedeli rozhodnúť, pozrime sa na to, ako sa mení celkový moment sily pôsobiaci na kyvadlo v závislosti od výchylky \[ M=-mgl\sin\phi+ml^{2}\Omega^{2}\sin\phi\cos\phi=ml\sin\phi\left(l\Omega^{2}\cos\phi-g\right)\text{.} \]

Kyvadlo je v rovnovážnej polohe, keď naň pôsobí nulový moment sily. Hneď vidíme, že poloha \(\phi_{0}=0\) je rovnovážnou polohou za každých okolností. Ako však naša analýza ukázala, je stabilná, t. j. umožňuje harmonické kmitanie, len kým \(\Omega<\sqrt{\frac{g}{l}}\), a potom sa stáva nestabilnou. Avšak pri prekročení tejto uhlovej rýchlosti sa objavuje nová rovnovážna poloha \(\phi_{0}=\arccos\frac{g}{l\Omega^{2}}\),⁴ ktorá je stabilnou, takže kyvadlo prejde do tejto novej polohy a bude okolo nej kmitať.

Ako bonus si skúste spočítať, že takéto kmitanie je naozaj možné. Na prvý pohľad sa to môže zdať ako totálny humus, ale je to naozaj spočítateľné. Hint: postup je úplne rovnaký, akurát výchylku tentokrát merajte od rovnovážnej polohy \(\phi_{0}\).

Komentár k riešeniam

Pri opravovaní som nenarazil na žiadnu chybu, ktorá by sa hromadne vyskytovala, preto by som tu chcel uviesť len dve poznámky.

Väčšina z vás na rozdiel od vzoráku riešila túto úlohu pomocou síl. Tento postup vás doviedol k správnemu výsledku, pretože sa jednalo o matematické kyvadlo. V prípade fyzikálneho kyvadla by ste sa však momentom síl a druhej vete impulzovej nevyhli. Preto odporúčam osvojiť si postup použitý vo vzoráku.

Po druhé by som vás chcel vyzvať, aby ste upravovali výsledky do ľudskejšej podoby. Isteže, výraz, ktorý je vďaka zloženým zlomkom na papieri vyšší než dlhší, s početnými odmocninami môže mať svoje čaro. Nechcem si ale predstaviť, ako ho nahadzujete do kalkulačky, keby ste chceli numerický výsledok. Týmto chcem pochváliť Legolasa, ktorý ako jediný myslel na opravovateľa a výsledok uviedol v stráviteľnom tvare.