5. Zase sústava vzorové riešenie

Zadanie

Jimi si zo svojej obľúbenej skrine vytiahol ďalšiu fakt kúl sústavu. Och… ale tentokrát to nebude žiaden grc! Teda aspoň podľa nemenovaného zdroja, ktorý tie grcy do tej skrine neustále vkladá…

A čože je to za sústavu? Recept na prípravu je nasledovný: Na dokonale navoskovanú podložku umiestnime dva hmotné body zo svojho obľúbeného obchodu s ideálnymi fyzikálnymi pomôckami, ktoré spojíme ideálnou pružinkou tuhosti \(k\) s pokojovou dĺžkou \(l\). Jedno z teliesok následne začneme ťahať silou \(F\) a ťahať neprestávame. Nuda, čo? Tak sa pokúste opísať pohyb oboch teliesok v čase.¹

---

1. V reči matematiky samozrejme. Klasické pokusy vymámiť od opravovateľa nejaké body za kopu prázdnych slov nespôsobia mnoho radosti ani na jednej strane ;-)↩

Riešenie tejto úlohy si rozdelíme do niekoľkých úvah, tak, aby každá z nich bola jednoduchá. Napriek tomu celok môže vyzerať komplikovane, aj keď to tak nie je ;-). Čo týmto celým chce autor vzoráku povedať? Že neradno preskakovať jeho časti a nad každou úvahou sa oplatí na chvíľku zastať a rozmyslieť si ju.

Úvaha prvá: ťažisková vzťažná sústava

Na začiatok pouvažujme, aké sily pôsobia na jednotlivé telieska spojené pružinkou. Okrem sily od pružinky sú to aj tiažové sily, tie sú však kompenzované normálovými silami. Keďže v zadaní sa spomína akási dokonale navoskovaná podložka, môžeme si v našich úvahách odpustiť aj trecie sily (ak by sme ich uvažovali, nevedeli by sme už len s pomocou papiera a pera dostať celú závislosť pohybu teliesok v čase). Jediné, čo nám teda zostalo, je zatiaľ neznáma sila od pružinky, ktorá pôsobí na každé teliesko a konštantná sila \(F\), ktorou napr. pravé teliesko ťaháme.

Prvý trik je nasledovný. Skúsme si predstaviť pomyselnú krabicu, ktorá obsahuje dve závažia hmotnosti \(m\) spojené pružinkou. Jediná sila, ktorá pôsobí na takúto krabicu, je konštantná sila \(F\) (sila od pružinky je už z hľadiska krabice vnútorná sila, čiže ak študujeme pohyb krabice ako celku, nevidíme jej prejavy). Ťažisko krabice (s hmotnosťou \(2m\)) sa teda bude hýbať iba pod vplyvom konštantnej sily \(F\), pôjde teda o priamočiary rovnomernerne zrýchlený pohyb so zrýchlením \(\frac{F}{2m}\). Keďže pružinky na začiatku stáli, tak aj počiatočná rýchlosť ťažiska je nulová. Ak si na opis pohybu teliesok zvolíme takú sústavu, pri ktorej je počiatočná pozícia ťažiska nulová (pre jednoduchosť, nič to nemení na výsledku), pozíciu ťažiska \(x_{\mathrm{T}}(t)\) v čase vieme zapísať ako \[ x_{\mathrm{T}}(t)=\frac{1}{2}\frac{F}{2m}t^2\text{.} \]

Ostáva nám už len vyriešiť, ako sa hýbu telieska vzhľadom na ťažisko. Kvôli tomu na chvíľu sústavu spojenú s ťažiskom opustíme. Znalí riešitelia fyzikálnych úloh by mohli nasledujúcu úvahu preskočiť, lebo si uvedomia, že aj v sústave spojenej so zrýchľujúcim ťažiskom platí zákon zachovania hybnosti. Ťažisko teda stojí na mieste (v sústave spojenej so zrýchľúcim ťažiskom), a teda keď je teliesko na pravo vzdialené od ťažiska o \(\chi\), tak aj teliesko naľavo je od ťažiska vzdialené o \(\chi\), len opačným smerom a rovno napíšu pohybovú rovnice pre telieska vyjadrené cez \(x_{\mathrm{T}}(t)\) a \(\chi\).

Úvaha druhá: pohyb teliesok v laboratórnej sústave

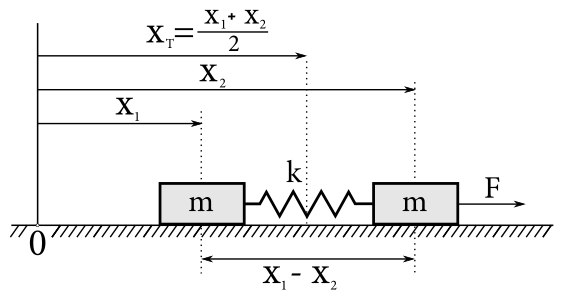
Tí z Vás, ktorí si tento trik nevšimli, nemusia zúfať, stačí sa len na telieska pozrieť v laboratórnej sústave. Označme pozíciu pravého telieska \(x_2(t)\) a polohu ľavého telieska \(x_1(t)\). Keďže majú rovnaké hmotnosti, pre ťažisko platí \[ x_{\mathrm{T}}(t) = \frac{x_1(t)+x_2(t)}{2}\text{.} \]

Analogický vzťah musí platiť¹ aj pre zrýchlenia ťažiska a jednotlivých teliesok, \[ a_{\mathrm{T}}(t) = \frac{a_1(t)+a_2(t)}{2}\text{.} \]

Skúsme si teraz napísať pohybové rovnice. Na druhé teliesko pôsobí sila \(F\) smerom doprava a sila \(k(x_2-x_1-l)\) doľava. \(x_2-x_1-l\) je totiž predĺženie pružinky voči pokojovej dĺžke \(l\). Na prvé telesko pôsobí len sila od pružinky \(k(x_2-x_1-l)\), ale opačným smerom: \[ ma_1 = k(x_2-x_1-l)\text{,} \] \[ ma_2 = F - k(x_2-x_1-l)\text{.} \]

Ak by sme tieto rovnice sčítali a predelili dvomi, dostaneme práve pohybovú rovnicu pre pohyb ťažiska (skúste si to sami urobiť). Čo teda môžeme ešte s rovnicami urobiť? Skúsme ich od seba odčítať a predeliť dvomi. Výraz \(\frac{x_2 - x_1}{2}\) bude potom práve už spomínané \(\chi\), t. j. pozícia druhého telieska voči ťažisku. Označme teda \[\chi(t) \equiv \frac{x_2(t)-x_1(t)}{2}\] a príslušný rozdiel zrýchlení ako \[ a_{\chi}(t) \equiv \frac{a_2(t)-a_1(t)}{2}\text{.} \]

Odčítaním rovníc a predelením dvomi získame \[ m\frac{(a_2-a_1)}{2} = \frac{F}{2} - 2k\left(\frac{x_2-x_1}{2} - \frac{l}{2}\right)\text{.} \] Čiže inak povedané \[ a_{\chi}(t) = \frac{F}{2m} - \frac{2k}{m}\left(\chi(t) - \frac{l}{2}\right)\text{.} \]

Zabudnime teraz na chvíľku, že máme nejaké dve telieska, v tejto rovnici máme už iba jednu pozíciu v čase \(\chi(t)\) a zodpovedajúce zrýchlenie \(a_{\chi}(t)\), prislúchajúce napr. nejakému pomyselnému teliesku. Ak by sme vedeli túto pohybovú rovnicu pre vzdialenosť teliesok voči ťažisku \(\chi(t)\) vyriešiť, tak už poznáme aj pohyb teliesok, keďže platí (skúste podumať alebo sa pozrieť na obrázok): \[ x_1(t) = x_{\mathrm{T}}(t) - \chi(t)\text{,} \] \[ x_2(t) = x_{\mathrm{T}}(t) + \chi(t)\text{.} \]

Úvaha tretia: pohyb teliesok voči ťažisku

Pustime sa do riešenia \[ a_{\chi}(t) = \frac{F}{2m} - \frac{2k}{m}\left(\chi(t) - \frac{l}{2}\right)\text{.} \]

Čo nám to pripomína? Rovnicu jednoduchého harmonického oscilátora. Čo nám tam ale vadí? Konštantná sila. Podumajme, ako to vyzerá na začiatku. Na začiatku sú obidve telieska v pokoji a pružinka má svoju pokojovú dĺžku \(l\). Obidve telieska majú rovnakú hmotnosť, takže sú obidve od ťažiska vzdialené o \(l/2\), preto je na začiatku \(\chi(t) = l/2\). Taktiež aj rýchlosti obidvoch teliesok sú nulové, aj voči ťažisku, a preto rýchlosť prislúchajúca \(\chi(t)\) je tiež rovná nule, \(v_{\chi}(t) = 0\). Rovnovážna dĺžka pružinky je \(l/2\).

Začneme teliesko ťahať. Čo sa stane? Okamžite sa zmení rovnovážna poloha pružinky. Prečo? Skúsme si predstaviť pokojne visiacu pružinku v gravitačnom poli a zavesme na ňu pomaličky závažie. Pružinka sa predĺži, no nebude kmitať (kvôli tlmeniu). Ak do pružinky drgneme, bude kmitať už okolo tejto novej polohy.

Ak teda na pružinku začne pôsobiť konštantná sila, rovnovážna poloha sa posunie. (Ako to môžeme vidieť inak v rovnici? Člen so silou \(F\) môžeme strčiť do zátvorky opisujúce predĺženie pružiny, stačí ho len rozšíriť a vydeliť vhodným výrazom). Teda nová pokojová dĺžka bude \(\frac{l}{2} + \frac{F}{4k}\). \[ a_{\chi}(t) = - \frac{2k}{m}\left(\chi(t) - \left(\frac{l}{2}+\frac{F}{4k}\right)\right)\text{.} \]

V tomto by sme už mali vidieť rovnicu jednoduchého harmonického oscilátora s \(\omega^2 = \frac{2k}{m}\), ktorý kmitá okolo rovnovážnej polohy \(\frac{l}{2} + \frac{F}{4k}\). Ako zistíme aká je nová rovnovážna poloha? Rovnovážna poloha je definovaná ako poloha, kedy na závažie pôsobí nulové zrýchlenie. Stačí sa teda pozerať, kedy je \(a_{\chi}(t) = 0\).

Keďže už poznáme frekvenciu harmonického oscilátora a rovnovážnu polohu, tak už vieme, že \(\chi(t)\) bude vyzerať nejako ako \[ \chi(t) = \left(\frac{l}{2}+\frac{F}{4k}\right) + A\sin\left(\sqrt{\frac{2k}{m}}t + \phi\right)\text{,} \] kde \(A\) je amplitúda a \(\phi\) je počiatočná fáza. Zostáva už teda určiť iba tieto dve veličiny. Na to sa pozrieme na tzv. počiatočné podmienky, t.j. to ako vyzerala vzdielnosť medzi telieskami (\(\chi\)) a ich vzájomná rýchlosť (\(v_{\chi}\)) v okamihu ako začneme ťahať jedno teliesko silou \(F\).

Na začiatku pohybu obidve telieska pokojne stoja na podložke (v laboratórnej sústave), dôležitá je ich však rýchlosť (\(v_{\chi}\)) v ťažiskovej sústave . Keďže však ťažisko na začiatku pohybu voči laboratórnej sústave stojí, tak a telieska sú v nej v pokoji, tak aj na základe zdravého sedliackeho rozumu, tušíme, že vzájomná rýchlosť teliesok je nulová. Taktiež vieme, že na začiatku sú telieska vzdialené od ťažiska o \(\chi = l/2\). Teraz si už len stačí uvedomiť, že teliesko na pružinke má nulovú rýchlosť v pozícii, ktorá zodpovedá maximálnemu natiahnutiu resp. stlačeniu pružinky.

Odtiaľ teda vieme, že amplitúda pohybu, t.j. ako ďaleko sa teliesko dostane od rovnovážnej polohy počas svojho pohybu je \[ \left| l/2 - \left(\frac{l}{2}+\frac{F}{4k}\right) \right| = \frac{F}{4k}\text{.} \] Už stačí len zistiť počiatočnú fázu \(phi\), na to si uvedomíme, že na začiatku pohybu sme v stave, kedy nulovú rýchlosť) a výchylku od rovnovážnej polohy \(-\frac{F}{4k} = \frac{l}{2} - \left(\frac{l}{2} + \frac{F}{4k}\right)\). Stav oscilátora s nulovou rýchlosťou zodpovedá maximálnej výchylke, preto bude amplitúda kmitov práve \(\frac{F}{4k}\). Pozícia kyvadla bude mať tendenciu narastať, odtiaľ teda určíme počiatočnú fázu kyvadla (počiatočná pozícia je záporná, preto narastá) ako \(\phi = 3\pi/2\)

Preto pre \(\chi(t)\) môžeme napísať \[ \chi(t) = \left(\frac{l}{2}+\frac{F}{4k}\right) + \frac{F}{4k}\sin\left(\sqrt{\frac{2k}{m}}t + \frac{3\pi}{2}\right) = \frac{l}{2} + \frac{F}{4k}\left(1-\cos\left(\sqrt{\frac{2k}{m}}t\right)\right)\text{.} \]

Pre pozície teliesok potom platí \[ x_1(t) = x_{\mathrm{T}}(t) - \chi(t) = \frac{1}{2}\frac{F}{2m}t^2 - \frac{l}{2} - \frac{F}{4k}\left(1-\cos\left(\sqrt{\frac{2k}{m}}t\right)\right)\text{,} \] \[ x_2(t) = x_{\mathrm{T}}(t) + \chi(t) = \frac{1}{2}\frac{F}{2m}t^2 + \frac{l}{2} + \frac{F}{4k}\left(1-\cos\left(\sqrt{\frac{2k}{m}}t\right)\right)\text{.} \]