5. Nabitá volejbalistka vzorové riešenie

Zadanie

Tánička zistila, že ju už frisbee nebaví (veď sa ani nehrá na letnej olympiáde), a tak sa dala na plážový volejbal. Aby to aj vyzeralo na úrovni, jej lopta s polomerom \(R\) bola pokrytá dvomi nevodivo spojenými polsférami alobalu. Bola šikovná a čo nevidieť sa v tom tak zlepšila, až jej to šlo lepšie ako frisbee¹ a porazila všetkých naokolo.

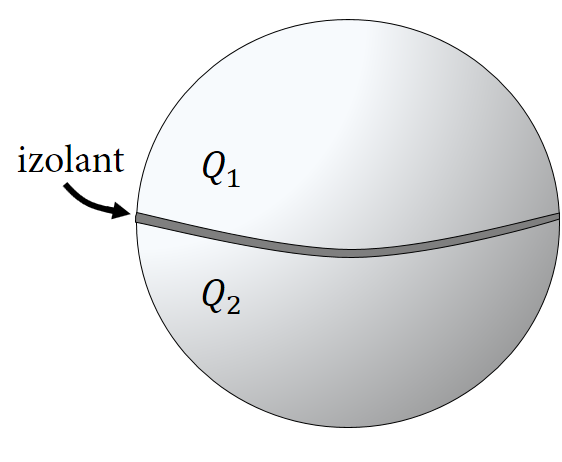
Tu však šla okolo Terka a napadlo jej, ako Táničku nabiť. Keď sa nikto nepozeral, nabila obe vodivé časti lopty na náboje \(Q_1\) a \(Q_2\). Vtom sa zarazila, lebo vedela, že priveľmi silné elektrické pole môže uškodiť okoliu. Rýchlo si preto spočítala, aké elektrické pole bude pred loptou v bode, ktorý je od stredu lopty vzdialený \(r\) a leží na rovine vytvorenej nevodivou vrstvou.

V zhone jej však vyšli rôzne výsledky. Skúste jej preto pomôcť a zistite, ktoré všetky majú v sebe chybu²:

1. \(E = \dfrac{1}{4\pi\epsilon_0} \dfrac{Q_1 Q_2}{r^2}\)
2. \(E = \dfrac{1}{4\pi\epsilon_0} \dfrac{\sqrt{Q_1 Q_2}}{r^2}\)
3. \(E = \dfrac{1}{4\pi\epsilon_0} \dfrac{|Q_1| + |Q_2|}{2 r^2}\)
4. \(E = \dfrac{1}{4\pi\epsilon_0} \dfrac{Q_1 + Q_2}{r^2}\)
5. \(E = \dfrac{1}{4\pi\epsilon_0} \dfrac{|Q_1 - Q_2|}{r^2}\)
6. \(E = \dfrac{1}{4\pi\epsilon_0} \left(\dfrac{Q_1 + Q_2}{2r^2} + \dfrac{Q_1 - Q_2}{2r^2}\right)\)
7. \(E = \dfrac{1}{4\pi\epsilon_0} \left(\dfrac{Q_1 + Q_2}{r^2} + \dfrac{|Q_1 - Q_2| R }{2r^3}\right) \ln^2{\dfrac{r^2}{4R^2}}\)
8. \(E = \dfrac{1}{4\pi\epsilon_0 r^2} \dfrac{Q_1^2 + Q_2^2}{{|Q_1| + |Q_2|}}\)
9. \(E = \dfrac{1}{4\pi\epsilon_0} \dfrac{|Q_1 - Q_2|}{R^2}\)
10. \(E = \dfrac{1}{4\pi\epsilon_0} \dfrac{|Q_1| + |Q_2|}{r^2} \sin{(2\pi r/R)}\)

Výsledok nemusíte odvodzovať, stačí ak správnou fyzikálnou intuíciou zistíte, ktoré výsledky sú zlé. Hodnotiť budeme najmä správnosť vašich argumentov, takže si na to dávajte pozor.

---

1. To bude zrejme tým, že plážový volejbal nepozná forehandy.↩

2. Aj keď je Terka nádejná budúca veľká fyzička, pod stresom to jednoducho nie je ona, takže chybu v sebe môžu mať aj všetky výsledky.↩

Toto je príklad v ktorom nebolo potrebné nič vypočítať, ale bolo treba sa dobre zamyslieť nad danými vzorcami a nájsť v nich chyby. Preto, ale toto ani zďaleka nie je jediné správne riešenie – možností bolo neúrekom. Tak, už by sme mohli začať.

Rozmerová analýza

Prvá vec, ktorá nám napadne pri kontrolovaní výsledkov, je rozmerová analýza. Intenzita elektrického poľa je sila na náboj, čiže každý zo vzorcov by mal byť v tvare: \[E = \dfrac{1}{4\pi\epsilon_0} \dfrac{q}{r^2}\text{,}\] alebo slovne: \[ E ~ \dfrac{1}{4\pi\epsilon_0} \dfrac{\text{coulomb}}{\text{meter}^2}\text{.}\]

Rýchlym pohľadom zisťujeme, že toto spĺňajú všetky vťahy okrem prvého, ktorý má namiesto Coulomba v menovateli súčin dvoch nábojov, čiže \(\text{Coulomb}^2\). Výsledok 1 teda môžeme vylúčiť.

Podozrivé výrazy: kvalitatívne závislosti na parametroch

Pozrime sa na výsledok 6. Sú tam zlomky so spoločným menovateľom! To znamená, že ich môžme sčítať a čo dostateneme je: \[ E= \dfrac{1}{4\pi\epsilon_0} \dfrac{Q_1}{r^2}\text{,} \] čo je výsledok ktorý nezávisí na náboji \(Q_2\). Toto je evidentne zle, takže výsledok 6 môžme tiež škrtnúť.

Ďalší podozrivý výsledok vyzerá byť 7., kôli logaritmu na konci. Logaritmus je funkcia, ktorá vracia nulu, keď je jej argument 1. Čiže pre \(r = 2R\) dostávame nulové elektrické pole. Avšak v tejto vzdialenosti je stále celý elektrický náboj na jedej strane, a teda nie je ničím kompenzovaný a elektrická intenzita by mala byť nenulová. Toto je spor, a preto je 7. výsledok nesprávny.

Posledný na prvý pohľad podozrivý vzorec je 9., lebo v menovateli sa nenachádza vzdialenosť od stredu, ale polomer lopty. Avšak ak sme od lopty dostatočne ďaleko, mala by sa nám javiť len ako náboj, čiže elektrické pole by malo so vzdialenosťou klesať. Výsledok 9 je teda taktiež zle.

Hodnoty nedávajúce zmysel

Ďalej sa poďme pozrieť, či nemáme nejaké vzorce, ktoré dávajú nelogické hodnoty. Intenzita elektrického poľa je síce vektorová veličina, no Terku zaujíma len veľkosť elektrického poľa, ktorá by nemala byť záporná.¹

Pozrime sa teda na to, ktoré výsledky môžu vracať záporné alebo nulové hodnoty intenzity. V prvom rade je to výsledok 2, v ktorom v prípade, že náboje majú opačné znamienka vo vnútri odmocniny získavame záporné číslo. Tí ktorí viete, odmocnina zo záporného čísla je komplexné číslo (to sú čísla, ktoré tvoria nadmnožinu množiny reálnych čísel). A to rozhodnie nie je to, čo očakávame pre intenzitu. Ak komplexné čísla nepoznáte, viete, že odmocnina zo záporného čísla nie je definovaná. V každom prípade výsledok 2 tiež nedáva zmysel pre konkrétne prípady, a preto je nesprávny.

Podobná situácia ako v predchádzajúcom odseku sa naskytá v 4. výsledku – ak oba náboje budú záporné, výsledná intenzita je záporná. Preto aj 4. je nesprávny.

A v neposlednom rade, výsledok 10 obsahujúci kladný výraz vynásobený sínusom nemôže byť správny, lebo sínus naberá kladné aj záporné hodnoty.

Dosadzovanie konkrétnych hodnôt

Zostávajú nám výsledky 3, 5 a 8. Skúsme do každého z nich dosadiť prípad \(Q = Q_1 = Q_2\). Pre výsledky dostávame intenzity \[ E_3 = \dfrac{1}{4\pi\epsilon_0} \dfrac{Q}{r^2}\text{,} \]

\[ E_5 = 0\text{,} \]

\[ E_8 = \dfrac{1}{4\pi\epsilon_0} \dfrac{Q}{r^2}\text{.} \]

Okamžite vidíme, že výsledok \(E_5\) nie je správny. Môžeme však niečo povedať aj o zvyšných dvoch výsledokoch? Predstavme si, že polomer lopty budeme zmenšovať, až bude blízky 0 – toto si môžme dovoliť, lebo výsledok nezávisí od \(R\). Vtedy efektívne dostávame bodový náboj, ktorého elektrické pole poznáme! Jedinú vec, na ktorú nesmieme zabudnúť je fakt, že náboje na oboch polsférach sa sčítajú, a teda budeme mať bodový náboj s veľkosťou \(2Q\). Ten má elektrické pole \[ E = \dfrac{1}{4\pi\epsilon_0} \dfrac{2 Q}{r^2}\text{,} \] čo nám ale nesedí ani s jedným s našich výsledkov a teda aj 3. a 8. výsledok sú nesprávne.

Iná možnosť bola dosadiť prípad \(Q_1 = -Q_2 = 0\). Pre tento prípad, by sme mali dostať pole elektrického dipólu, ktoré klesá ako \(1/r^3\).

Žiaden z výsledkov teda bohužial nie je správny. My však Terke aj tak stále veríme.