Zadanie
Vladko sa dočítal, že to bol práve Kepler, kto objavil tri zákony pohybu planét. Avšak tak, ako ich poznal on, sa dajú použiť iba vtedy, keď je obežnica (planéta, mesiac, atď.) omnoho ľahšia ako centrálne teleso (hviezda, planéta, atď.).
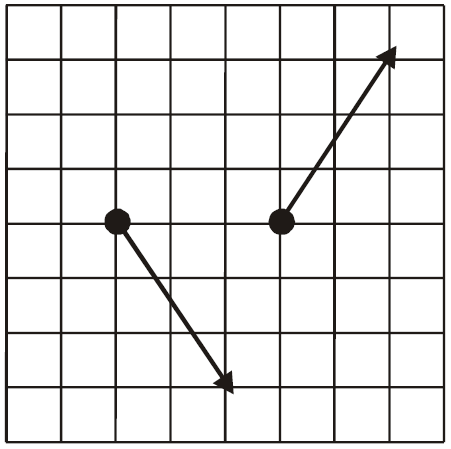
Vladko však dostal od Peťa na úlohu z mechaniky vypočítať periódu obehu dvojhviezdy okolo spoločného ťažiska. Peťova dvojhviezda sa skladá z hviezd s podobnými hmotnosťami \(M\) (vľavo na obrázku) a \(2M\) (vpravo na obrázku). Vyriešte túto úlohu za pomoci Keplerových zákonov a elementárnej fyziky. Dĺžka jedného dielika je \(l\), rýchlosti hviezd v jednom okamihu sú také ako na obrázku (jeden dielik zodpovedá rýchlosti \(v\)). Peťo Vladkovi prezradil, že navyše platí \(GM = 24lv^2\), kde \(G\) je gravitačná konštanta.
Pozrime sa na najprv na tri Keplerove zákony, ktoré – ako vieme zo zadania – objavil už aj Vladko:
- Planéty obiehajú okolo Slnka po eliptických trajektóriách s malou výstrednosťou, pričom Slnko sa nachádza v jednom spoločnom ohnisku.
- Sprievodič (spojnica Slnka a planéty) opíše za rovnaký čas vždy rovnakú plochu (prakticky zákon zachovania momentu hybnosti).
- Druhé mocniny obežných dôb planét pri ich obiehaní okolo Slnka sú úmerné tretím mocninám hlavných poloosí ich eliptických dráh.
Kepler predpokladal, že stred Slnka je totožný s hmotným stredom slnečnej sústavy a ten sa nehýbe. To nás vedie k tomu, aby sme sa venovali najprv hmotnému stredu našej dvojhviezdy. Označme rýchlosť hviezdy naľavo v obrázku v zadaní \(\vec{v_1}\) a hviezdy napravo \(\vec{v_2}\). Keďže jednému dieliku prislúcha podľa zadania veľkosť rýchlosti \(v\), po zavedení vhodnej súradnicovej sústavy (\(x\)-ová súradnica v smere zľava doprava, \(y\)-ová súradnica v smere zdola hore) vieme určiť vektory \(\vec{v_1} = (2v, -3v)\) a \(\vec{v_2} = (2v, 3v)\).
Rýchlosť hmotného stredu \(\vec{v_{\mathrm{t}}}\) určíme zo zákona zachovania hybnosti,Vidíme, že hmotný stred sústavy sa pohybuje, ale tento problém vieme ľahko vyriešiť tak, že sa presunieme do inerciálnej sústavy, kde hmotný stred sústavy stojí. Potom pre rýchlosti hviezd dostávame \(\vec{v_1}' = \vec{v_1} - \vec{v_{\mathrm{t}}} = (0, -4v)\) a \(\vec{v_2}' = \vec{v_2} - \vec{v_{\mathrm{t}}} = (0, 2v)\). Ľahký výpočet prezradí, že hmotný stred sa nachádza v dvoch tretinách vzdialenosti medzi hviezdami od hviezdy naľavo.
Situácia teraz v sústave spojenej s hmotným stredom vyzerá nejako takto:

Na obe hviezdy pôsobí gravitačná sila veľkosti \(F_g = G\frac{2M^2}{(3l)^2}\), kde \(3l\) je vzájomná vzdialenosť medzi hviezdami a \(G\) je gravitačná konštanta. Keďže úlohu chceme vyriešiť za pomoci Keplerových zákonov, a tie možno použiť iba v prípade, ak jeden z objektov je rádovo ťažší ako druhý, a teda sa vplyvom gravitačnej sily prakticky nehýbe, musíme situáciu znovu transformovať. Oba objekty teraz obiehajú okolo spoločného hmotného stredu. Hmotný stred sa nemôže hýbať inak ako rovnomerným priamočiarym pohybom, ale takýto pohyb sme už zakázali presunutím sa do vhodnej sústavy.
Ďalej si všimnime, že gravitačná sila, ktorá pôsobí na hviezdu napravo, spôsobená silou naľavo, má veľkosť \[ F_g = G\frac{2M^2}{r^2}\text{,} \]
kde \(G\) je gravitačná konštanta a \(r\) je vzájomná vzdialenosť medzi hviezdami. Vzájomná vzdialenosť medzi hviezdami sa môže meniť, ale pozícia hmotného stredu je už v našej sústave fixovaná. To inak povedané znamená, že nech je vzájomná vzdialenosť hviezd \(r\) akákoľvek, hmotný stred bude vždy ležať na spojnici hviezd, v tretine ich vzdialenosti od ťažšej hviezdy.
Urobme preto teraz nasledujúci myšlienkový experiment. Odstráňme zo systému hviezdu naľavo a nahraďme ju virtuálnou hviezdou ležiacou na pozícii hmotného stredu pôvodonej dvojhviezdy s takou hmotnosťou \(m\), aby gravitačný účinok virtuálnej hviezdy na hviezdu napravo bol rovnaký, ako od pôvodnej hviezdy naľavo. Ak zvolíme \(m = M/9\), ľahko sa presvedčíme, že dostaneme rovnakú silu, nech je \(r\) akékoľvek. \[ F_g = G\frac{2M(M/9)}{(r/3)^2} = G\frac{2M^2}{r^2}\text{.} \]
Ak teraz umelo zafixujeme virtuálnu hviezdu na tomto mieste, gravitačná sila od virtuálnej hviezdy bude mať vždy správny smer aj veľkosť, ako od pôvodnej hviezdy naľavo. Ak sa obmedzíme iba na štúdium pohybu hviezdy napravo, môžeme smelo používať Keplerove zákony a nájsť periódu obehu ťažšej hviezdy okolo spoločného hmotného stredu oboch hviezd.
Pred tým, než sa pustíme do riešenia, si iba v krátkosti vysvetlime, prečo je spomínaný krok legálny. Hviezda napravo „netuší“, čo spôsobuje silu, ktorá na ňu pôsobí. Ak však zabezpečíme, že je presne rovnaká (veľkosťou aj smerom), ako keby tam boli obe hviezdy, hviezda napravo sa musí nutne hýbať rovnako, ako keby tam tie hviezdy boli obe. Newtonove zákony jednoznačne určujú budúcnosť systému na základe počiatočných podmienok a tie sú rovnaké, takže aj časový vývoj polohy hviezdy napravo musí byť rovnaký. Poznamenajme, že virtuálnej hviezde sme zakázali pohyb a našou konštrukciou nenarušíme zákon zachovania energie (ten musí byť splnený, lebo máme správnu silu) a aj zákon zachovania momentu hybnosti (v našom prípade sa zachováva aj moment hybnosti každej hviezdy samostatne. Rozmyslite si prečo.)
Teraz môžeme smelo používať všetky finty, ktoré už dávno poznáme, stačí ak budeme študovať len pohyb ťažšej hviezdy v poli virtuálnej hviezdy s \(m = M/9\), ktorá vždy stojí na mieste.
Periódu obehu ľahko zistíme z tretieho Keplerovho zákona, ak budeme poznať dĺžku hlavnej polosi elipsy, po ktorej obieha ťažšia hviezda okolo spoločného hmotného stredu hviezd. Z úvahy vyššie vieme, že v jednom z ohnísk bude ležať nehybná virtuálna hviezda. Dĺžku hlavnej polosi ľahko určíme zo zákona zachovania mechanickej energie a zákona zachovania momentu hybnosti (čo je druhý Keplerov zákon až na nejakú tú polovicu). Celková mechanická energia sústavy \(E_0\) je súčtom potenciálnej a kinetickej energie v hociktorom čase (takže napríklad aj vo východzej situácii). Nulový potenciál gravitačného poľa virtuálnej hviezdy môžeme voliť v nekonečne, a dostávame \[ E_0 = \frac{1}{2}2M(v_2')^2 - G\frac{2M(m/9)}{(r/3)} = 4Mv^2 - G\frac{2M^2}{9l} = -\frac{4}{3}Mv^2\text{,} \]
kde sme využili vzťah zo zadania \(GM = 24lv^2\).
Z obrázka vidno, že aktuálny smer rýchlosti je kolmý na spojnicu hviezd. Takáto situácia môže nastať iba v pericentre alebo apocentre. Súčet vzdialeností medzi ťažšou hviezdou a virtuálnou hviezdou v pericentre a apocentre je rovný presne dvojnásobku hlavnej poloosi elipsy, po ktorej ťažšia hviezda obieha.

V prípade pericentra vieme, že \(r = l\) a \(\lvert\vec{v_2'}^2\rvert = 2v\), v apocentre si označíme vzdialenosť ako \(\rho\) a rýchlosť ako \(v_{\rho}\). Z druhého Keplerovho zákona \[ 2M \cdot 2v \cdot l = 2M \cdot \rho \cdot v_{\rho} \implies v_{\rho} = 2vl/\rho\text{.} \]
Dosadením do zákona zachovania energie dostaneme rovnicu \[ \frac{1}{2}2M{v_{\rho}}^2 - G\frac{2M^2}{9\rho} = E_0\text{,} \] do tejto rovnice môžeme vložiť následne vypočítanú hodnotu \(E_0\), za \(v_{\rho}\) dosadíme hodnotu z vypočítanú z 2. Keplerovho zákona a nakoniec využitím \(GM = 24lv^2\) získame rovnicu \[ (\rho-l)(\rho-3l) = 0\text{.} \]
Riešenie \(\rho = l\) je pericentrom a zodpovedá počiatočnému stavu v nami skonštruovanej sústave. Riešenie \(\rho = 3l\) je apocentrom. Odtiaľto už vidíme, že dĺžka hlavnej polosi je \((l+3l)/2 = 2l\).
Využitím tretieho Keplerovho zákona (ten môžeme použiť, lebo predpokladáme, že virtuálna hviezda počas celého pohybu stojí), \[ T^2 = \frac{4\pi^2 a^3}{Gm} = \frac{4\pi^2 (2l)^3}{G(M/9)} = \frac{4\pi^2 \cdot 72l^3}{24lv^2} \implies T = 2\pi\frac{\sqrt{3}l}{v}\text{.} \]
Dostaneme periódu \(T\) obehu ťažšej hviezdy okolo spoločného hmotného stredu. Keďže hmotný stred sa nemôže hýbať, perióda obehu ľahšej hviezdy okolo hmotného stredu musí byť rovnaká.
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.