4. Naladený čajník vzorové riešenie

Našou úlohou je zmerať závislosť frekvencie zvuku v pohári s vodou od teploty. V prvom rade si musíme vyjasniť, čo rozumieme pod pojmom frekvencia pohára s vodou. Zvuk šíriaci sa prostredím je v podstate tlaková vlna. Frekvencia zvuku nám popisuje, ako sa tento tlak mení v závislosti od času. Avšak bežné zvuky v prírode sa neskladajú iba z jednej vlny s konkrétnou frekvenciou, ale z nekonečného množstva vĺn s rôznymi frekvenciami a intenzitami (amplitúdami), čiže nemá jedinú presne definovanú frekvenciu. Keď natiahneme strunu a pustíme ju, táto struna začne vibrovať, pričom interakciou so vzduchom rozvibruje aj ten, a vzduchom sa začne šíriť zvuková vlna so spektrom¹ zodpovedajúcim spektru struny.

Vysvetliť, prečo bude spektrum struny práve také, aké bude, nie je úplne jednoduché. V úplne primitívnom modeli si povedzme, že keď struna kmitá, správa sa ako sínus, ktorý je na koncoch nulový, keďže na tomto mieste je struna pripevnená. Tomuto zodpovedajú funkcie z rodiny \(\sin{\frac{\pi x}{\lambda}}\sin{\frac{vt}{\lambda}}\), kde \(x\) je poloha na strune a \(v\) rýchlosť zvuku v nej. Keďže sínus musí byť nulový na koncoch struny, pre \(\lambda\) musí platiť \(\lambda=\frac{2 L}{n}\), kde \(L\) je dĺžka struny a \(n\) ľubovoľné prirodzené číslo. Odtiaľ vieme frekvenciu vyjadriť ako \(f=\frac{n v}{2 L}\). Nad celým týmto postupom si nemusíte veľmi lámať hlavu, pretože bol veľmi nepresný, ale poslúžil nám na ilustráciu pre nás dôležitého faktu, že zvuk struny sa skladá iba z násobkov určitých frekvencií. Zastúpenie týchto frekvencií vieme ovplyvňovať napríklad tým, ako silno vybudíme strunu.

Ak našu úvahu zovšeobecníme pre hrnček s vodou, jeho zvukové spektrum bude zložené taktiež iba z určitých frekvencií, ale toto spektrum bude úplne divoké, vzhľadom za zložitý tvar hrnčeka. Vďaka vlastnostiam materiálu a vody budú určité frekvencie šíriace sa naším systémom takmer ihneď po vybudení utlmené,² zatiaľ čo iné frekvencie sa zachovajú. Tieto zvyšné frekvencie, ktoré sa neutlmia, nazývame prirodzenými frekvenciami systému, a budú výrazne intenzívnejšie ako iné. Práve tieto frekvencie budú charakteristické pre náš systém a ich závislosť od teploty sa budeme snažiť namerať. Keď sme si objasnili aspoň základný koncept nášho systému, môžeme sa pustiť do merania.

Spektrum sa bude divoko meniť v závislosti na viacerých parametroch. Preto sa budeme snažiť všetky fixovať, samozrejme okrem teploty. Aby sa nám meralo čo najlepšie, je výhodné si zvoliť čo najjednoduchší hrnček. Budiť ho budeme úderom lyžičkou na to isté miesto.³ My sme si zvolili hrnček takmer valcovitého tvaru. V rýchlovarnej kanvici sme zohriali vodu a naliali do hrnčeka. Od tohoto okamihu sme vodu nepridávali ani neodoberali, iba ju nechali chladnúť, aby sme spolu s objemom vody zbytočne nemenili parameter navyše.

Teplomerom sme zmerali teplotu vody. Použili sme klasický ortuťový teplomer so stupnicou od \(\SI{0}{\celsius}\) do \(\SI{100}{\celsius}\). Pre jednu teplotu sme udreli na hrnček viackrát, a pomocou softvéru Audacity sme zaznamenali zvuk, ktorý hrnček vydal. Samozrejme, teplota sa počas procesu menila, ale keďže celé meranie netrvalo viac ako pár sekúnd, predpokladali sme, že teplota bola konštantná. Potom sme počkali, kým sa voda neochladí o pár stupňov a celý folklór zopakovali.

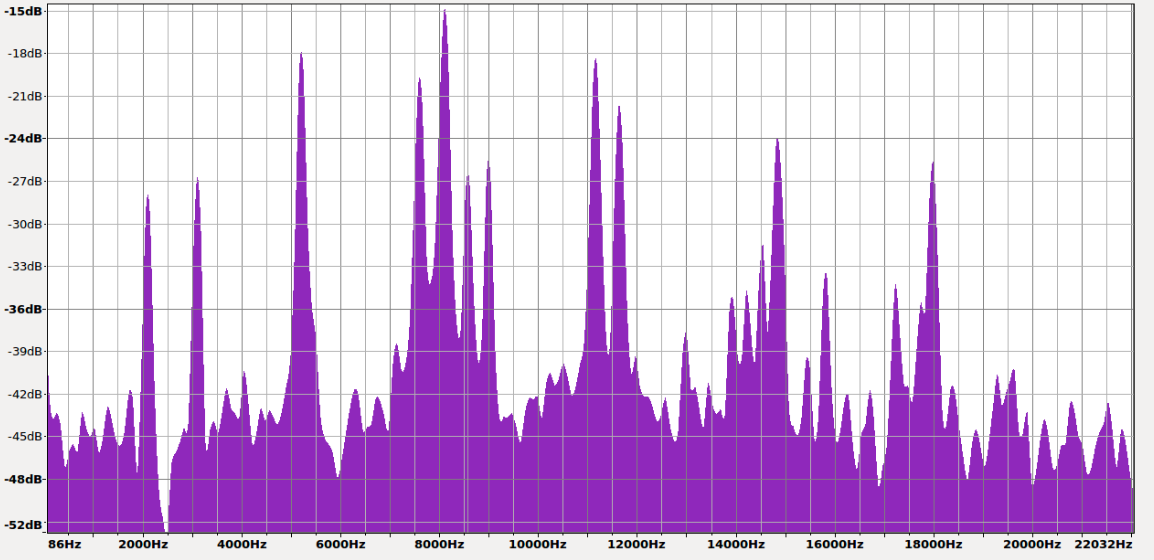
Analýzou zvukových nahrávok v Audacity sme získali frekvenčné spektrá. Z frekvenčných spektier sme určili polohu prvého najvýraznejšieho vrcholu. Vhodné by bolo odčítať najvýraznejší vrchol celkovo, avšak tento sa odčítava oveľa komplikovanejšie, vzhľadom na vysoké nepresnosti nášho merania. Podľa šírky vrcholu vieme približne určiť, ako presne meriame. Je vhodné urobiť čo najviac meraní.

Chyby pri meraní vznikajú v dôsledku nekonštantnej budiacej sily, problematického určenia maxima, odparovania vody, šumu okolia, teplotnej roztiažnosti hrnčeku a vody… taktiež zloženie vody môže byť problém, pretože frekvencia môže závisieť od koncentrácie rozpustených látok.

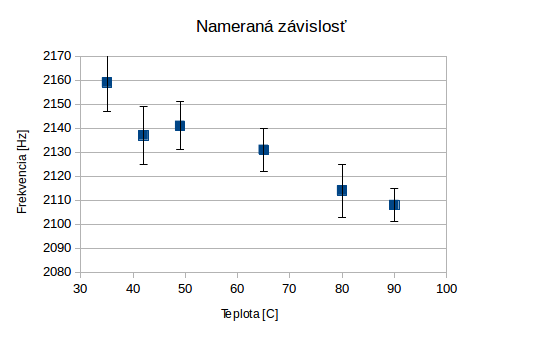
Skúsme sa teraz zamyslieť, prečo závislosť, ktorú sme namerali, vyzerá práve takm ako vyzerá. Pre frekvenciu platí \[f=\frac{v}{\lambda}\text{.}\]

Otázkou ostáva, ako sa menia vlnové dĺžky a rýchlosť zvuku vo vode s teplotou. Vo všeobecnosti toto môže závisieť od troch faktorov: hustoty vody, stlačiteľnosti vody a jej teplotnej rozťažnosti. Napríklad v oceli, ktorá je málo stlačiteľná a hustejšia, sa pohybuje zvuk omnoho rýchlejšie ako vo vzduchu, ktorý je ľahko stlačiteľný a redší. Najprv hrubo odhadnime vplyv hustoty a roztiažnosti. Vieme alebo si nájdeme, že rýchlosť zvuku vo vode je úmerná \(v=\sqrt{\frac{K}{\rho}}\), kde \(K\) je člen zahŕňajúci stlačiteľnosť vody, a \(\rho\) je hustota vody. Predpokladajme, že hustota sa mení iba vplyvom teplotnej roztiažnosti. Potom \[v=\sqrt{\frac{K V}{m}}\text{,}\] kde \(V\) je objem.

Objem vody sa mení ako \(V=V_0 \left(1 + \beta \Delta T\right)\). Predpokladajme, že aj vlnová dĺžka sa mení úmerne objemu, \[\lambda \propto \lambda_0 \left(1 + \beta \Delta T \right)\text{.}\]

Kombináciou týchto vzťahov dostávame \[f \propto \frac{1}{\sqrt{\left(1 + \beta \Delta T \right)}}\text{.}\]

Toto súhlasí s našou nameranou závislosťou.

Čo sa týka stlačiteľnosti, nastáva jav nazývaný Hot Chocolate Effect, aj keď pre vodu namiesto čokolády by sa dal nazvať obrátený Hot Chocolate Effect.⁴ Pointou je, že rýchlosť zvuku vo vode závisí najmä na dvoch veciach, hustote a stlačiteľnosti.

Hustota s teplotou klesá, a vďaka tomu by mala rýchlosť narastať. Avšak v horúcej vode sa náchádza veľa vzduchových bubliniek. Vdaka týmto bublinkám bude voda oveľa stlačiteľnejšia, a zvukové vlny, ktoré sa šíria stláčaním a rozpínaním vody, sa budú pohybovať pomalšie. Tento jav, teda taktiež podporuje pokles frekvencie.

Na záver prikladáme veľmi pekne nameranú závislosť aj s teoretickou predpoveďou od Mišky Leinwatherovej.