5. Sánkovačka vzorové riešenie

Najprv si skúsme uvedomiť, aké sily na kváder pôsobia. Budú to tiažová sila \(F_g\), normálová sila od podložky \(F_n\) a trecia sila \(F_t\). Tiažovú silu môžeme rozdeliť na dve zložky – kolmú na naklonenú rovinu (jej účinok je vyrovnaný s účinkom normálovej sily \(F_n\)) a rovnobežnú s rovinou (v smere najväčšieho poklesu), označíme ju \(F_r\). Rozložením síl zistíme, že kolmá zložka má veľkosť \(F_n = m g \cos{\alpha}\) a rovnobežná má veľkosť \(F_r = m g \sin{\alpha}\).

Pre treciu silu platí, že jej veľkosť je \(F_t = f F_n\),¹ čo v našom prípade znamená, že \(F_t = m g \cos{\alpha} \tan{\alpha} = m g \sin {\alpha}\). Jej smer je proti pohybu kvádra – t. j. proti smeru vektora aktuálnej rýchlosti. Tento výsledok je zaujímavý, lebo zisťujeme, že veľkosť sily \(F_t = F_r\).

Teraz už vieme, že na kváder pôsobia dve sily spôsobujúce dvojicu zrýchlení – jedného smerom nadol² a jedného proti smeru jeho pohybu. Ako teda spolu pôsobia na sústavu? Pozrime, čo sa udeje za krátky čas \(\Delta t\). Zaň stihne trecia sila zmenšiť celkovú rýchlosť \(v_c\) kvádra o \(\Delta v_c = \frac {F_t}{m} \Delta t\), zatiaľ čo pozdĺžna zložka tiažovej sily zväčší pozdĺžnu časť rýchlosti \(v_y\) o \(\Delta v_y = \frac {F_y}{m} \Delta t\). Tu si spomeňme, že \(\left|F_r\right| = \left|F_t\right|\). To ľudskou rečou znamená, že o koľko sa zmenší celková rýchlosť kvádra, o toľko sa zvýši pozdĺžna zložka tejto rýchlosti. Matematicky zapísané \(v_c + v_y = C\), kde \(C\) je konštanta.

V pohode? No nie tak rýchlo! Je tu totiž istá zrada, ktorá si zaslúži nasledujúce úvahy. Na chybu vo vzoráku nás upozornil Filip Čermák, za čo mu na tomto mieste veľmi pekne a úprimne ďakujeme.

Chyba v tejto úvahe je totiž v tom, že platí síce, že \(\left|F_r\right| = \left|F_t\right|\), ale už nie je pravda, že \(\Delta v_c = \frac {F_t}{m} \Delta t\) (Správne to má byť \(\Delta v_c = \frac {F_t-F_{rz}}{m} \Delta t\) kde \(F_{rz}\) je istá zložka sily \(F_t\)). Do zmeny celkovej rýchlosti totiž okrem samotnej trecej sily prispieva aj sila \(F_r\), ktorá vždy pôsobí tým istým smerom, ktorý nie je zhodný s \(F_t\). Môžete si rozmyslieť, že tvrdenie \(v_c + v_y = C\) platí v prvých fázach pohybu, ked je sila \(F_t\) kolmá na \(v\), no nie je vôbec jasné, že bude platiť vždy. Nerobme preto žiadne unáhlené závery a skúsme naozaj poctivo dokázať, že \(v_c + v_y = C\).

Pozrieme sa teraz, čo sa udeje s kvádrom za malý čas \(\Delta t\). Napíšme si teda pohybové rovnice pre pohyb kvádra. Celkovú rýchlosť kvádra môžeme rozložiť do spomínaných smerov na zložky \(v_x\) a \(v_y\). Keďže trecia sila \(F_t\) pôsobí proti smeru aktuálnej rýchlosti \(v_c\), má zložku v obidvoch smeroch. Veľkosť zložky trecej sily v danom smere je úmerná veľkosti zložky rýchlosti ku celkovej rýchlosti kvádra v danom smere (vyplýva to z jednoduchej geometrie – viď obrázok).

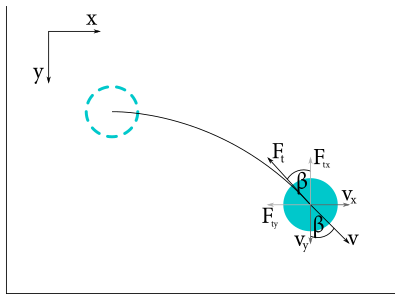
Preto zložky trecej sily v jednotlivých smeroch sú \[\begin{align*} F_{\mathrm{tx}} &= F_t \sin{\beta} = F \frac{v_x}{v_c}\text{,}\\ F_{\mathrm{ty}} &= F_t \cos{\beta} = F \frac{v_y}{v_c}\text{.} \end{align*}\] Napíšme si teraz pohybové rovnice pre pohyb kvádra v smere najstrmšieho poklesu výšky (\(y\)) a v kolmom smere naň (\(x\)). \[\begin{align*} a_x &= \frac{\Delta v_x}{\Delta t} = -\frac{F_{\mathrm{tx}}}{m} = \frac{F}{m}\left(-\frac{v_x}{v_c}\right)\text{,}\\ a_y &= \frac{\Delta v_y}{\Delta t} = \frac{F_r}{m}-\frac{F_{\mathrm{ty}}}{m} = \frac{F}{m}\left(1-\frac{v_y}{v_c}\right)\text{.} \end{align*}\] Skúsme si teraz ešte vypočítať, ako súvisí zmena celkovej rýchlosti \(\Delta v_c\) so zmenou jej zložiek v \(y\)-ovom (\(\Delta v_y\)) a \(x\)-ovom smere (\(\Delta v_x\)). Vieme, že platí \(v_c^2 = v_x^2 + v_y^2\). Ide teda o Pytagorovu vetu. Pre lepšiu predstavivovosť sa nám zíde nasledujúca geometrická interpretácia. Predstavme si pravouhlý trojuholník s preponou dĺžky \(c\) a odvesnami s dĺžkami \(a\) a \(b\).

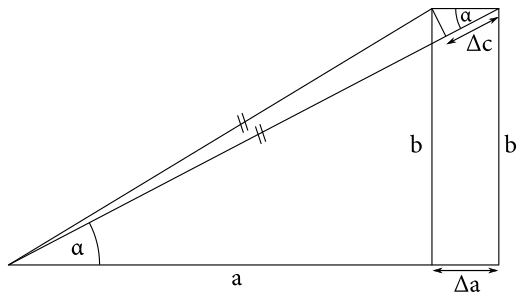
Pre pravouhlý trojuholník platí Pytagorova veta \(c^2 = a^2 + b^2\). Ak zväčšíme jednu odvesnu o \(\Delta a\), odvesna sa zväčší (podobnosť trojuholníkov) o (približne) \[ \Delta c = \Delta a \cos(\alpha) = \frac{a}{c} \Delta a\text{,} \]

Pre tých z Vás, ktorý majú radšej výpočty: k rovnakému výsledku sa dopracujeme, ak od \({\left(c+\Delta c\right)}^2\) odpočítame \(c^2\) a zanedbáme \({\left(\Delta c\right)}^2\) a \({\left(\Delta a\right)}^2\)³, \[\begin{align*} {\left(c+\Delta c\right)}^2 - c^2 &= \left({\left(a+\Delta a\right)}^2 + b^2\right) - \left(a^2 + b^2\right)\text{,}\\ c^2 + 2c\Delta c + {\Delta c}^2 - c^2 &= \left(a^2 + 2a\Delta a + {\Delta a}^2\right) - \left(a^2 + b^2\right)\text{,}\\ 2c\Delta c &\approx 2a\Delta a\text{,}\\ \Delta c &\approx \frac{a}{c}\Delta a\text{.} \end{align*}\]

Obe úvahy môžeme rozšíriť aj na druhú odvesnu, a preto \[ \Delta v_c = \frac{v_x}{v_c}\Delta v_x + \frac{v_y}{v_c}\Delta v_y\text{.} \]

Skúsme teraz vypočítať, čomu je rovné \(\Delta v_c + \Delta v_y\). Ak nám víde, že je to nula, tak sme vyhrali, lebo potom musí platiť, že súčet \(v_y + v_c\) je konštantný. \[\begin{align*} \Delta v_c + \Delta v_y &= \left(\frac{v_x}{v_c}\Delta v_x + \frac{v_y}{v_c}\Delta v_y\right) + \Delta v_y = \left(-{\left(\frac{v_x}{v_c}\right)}^2\frac{F}{m} + \frac{v_y}{v_c}{\left(1-\frac{v_y}{v_c}\right)}\frac{F}{m}\right) + {\left(1-\frac{v_y}{v_c}\right)}\frac{F}{m}\text{,}\\ &= -{\left(\frac{v_x^2}{v_c^2}\right)}\frac{F}{m} + \left(1-\frac{v_y}{v_c}\right)\left(1+\frac{v_y}{v_c}\right)\frac{F}{m}\text{,}\\ &= \left(1-\frac{v_x^2+v_y^2}{v_c^2}\right)\frac{F}{m} = 0\text{,} \end{align*}\] keďže \(v_x\) a \(v_y\) sú iba zložky \(v_c\), a teda \(v_c^2 = v_x^2 + v_y^2\). Naozaj teda platí \(\Delta v_c + \Delta v_y = 0\), a to vo všetkých fázach pohybu! Preto sa súčet \(v_c + v_y\) zachováva. Teda matematicky zapísané (\(C\) je konštanta): \[ v_c + v_y = C\text{!} \]

Na začiatku pohybu je \(v_y = 0\) a \(v_c = \sqrt{v_x^2+v_y^2} = v_x = v\), preto \(C = v\). Teraz potom, čo sme si už naozaj poctivo dokázali tvrdenie \(v_c + v_y = C\), sa pozrime sa na ustálený stav pohybu kvádra. Ten nastane vtedy, keď sa sily naň pôsobiace vyrovnajú. No, a to sa stane iba v prípade, keď sa kváder bude hýbať v smere najväčšieho poklesu (áno, bude to trvať nekonečne dlho). Vzťah pre rýchlosť \(v_c + v_y = v\) bude platiť aj vtedy. Teda platí \(v_c = v_y\), lebo \(v_c\) má iba zložku v smere najstrmšieho poklesu výšky na naklonenej rovine. Preto môžeme dosadiť \(v_y + v_y = 2 v_y = C = v\), a teda \(v_y\) v ustálenom stave je rovná \(v/2\).

Takto sme zistili, že po dlhom čase bude mať rýchlosť rovnaký smer, ako je smer najväčšieho poklesu a jej veľkosť bude \(\frac{v}{2}\). Ešte by ste sa mohli spýtať, či by kváder nemohol počas svojho pohybu zastať. Sila \(F_r\) však pôsobí neustále, a až keď nastane ustálený stav, jej smer sa vyrovná so silou \(F_t\), a preto v každom okamihu urýchľuje kvádrik v smere najstrmšieho poklesu výšky, čím mu bráni v tom, aby sa zastavil.

Poznámka pre simulantov v Exceli a podobné tvory

Mnoho z Vás sa numerickou simuláciou dopracovalo k správnemu výsledku. A zistili ste, že v takom prípade, nech je \(\alpha\) akékoľvek, výsledok to neovplyvní. V tomto okamihu by ste mali spozornieť, pretože sa tu deje niečo podozrivé. Navyše podozrivá je aj jedna polovica. Odteraz by Vám mala v hlave svietiť kontrolka, že ak je výsledok jednoduchý, je možné, že sa k výsledku dá dopracovať aj s použitím papiera a pera.

Poznámka pre drtičov, dostatočne skazených deriváciami, integrálmi či diferenciálnymi rovnicami

Niekedy je riešenie fyzikálneho problému naozaj jednoduché, no vyžaduje si to dostatočnú pozornosť na všetky detaily problému a dôsledné uvedomenie si toho, čo tieto fakty naozaj znamenajú.