4. Hodina plávania vzorové riešenie

Pred samotným vyhotovením experimentu a získavaním dát je vhodné zamyslieť sa, či by sme vedeli a boli ochotní vysloviť nejaký teoretický predpoklad alebo odhad. Okrem iného je to vhodné i takým spôsobom, že ak tušíme, ako by mal výsledok experimentu vyzerať, vieme si samotný experiment lepšie navrhnúť, napríklad vyvarovať sa meraniu závislostí na málo zaujímavých intervaloch parametrov (na Štrbskom plese, Zlatých pieskoch a pri Kaspickom mori), zvoliť vhodný tvar nádob i oscilátora samého (hruška v karafe). Takisto môžeme porovnať naše výsledky s predpokladom, a tým zistiť, či sme niečo zmrvili, čosi opomenuli, alebo zistíme, že náš model je zlý.

Majme objekt zatiaľ pokojne právajúci vo vode. Z jeho krotkosti vieme vyčítať, že je v rovnováhe nielen duševnej, ale i dynamickej (t. j. silovej). Pretože časť predmetu trčí nad vodou, na situáciu sa vieme pozrieť dvomi spôsobmi (v zásade rovnakými, len s mierne odlišnou terminológiou a úrovňou všeobecnosti). Tiažová sila je pre dané teleso v rovnováhe so silou vztlakovou, resp. tlakovou silou na spodok spomínaného marazmu (tu sa patrí podotknúť že za vhodné teleso a nádobu pre teoretickú úvahu aj experiment je rozumné považovať také s vodorovnou podstavou, zvislými bočnými stenami a pre teleso aj ťažiskom nachádzajúcim sa na rovnakej zvislici ako jeho geometrický stred).

Ak vyvediem teleso z rovnováhy čímsi fyzickejším ako nepríjemnou otázkou (napr. ako sa pričiňuje k zníženiu štátneho schodku), pre naše potreby ideálne potlačením do vody, v prvom pohľade sa mi zväčší objem telesa pod hladinou a teda aj vztlaková sila, v druhom spôsobe pohľadu sa mi podstava posunie hlbšie, kde je vyšší tlak, a teda aj tlaková sila na ňu. Podotýkam, tieto veci sú ekvivalentné ak je vršok telesa vždy nad hladinou.

Zaujímavejšia časť teoretického základu tejto úlohy je ale o tom, čo sa stane s vodou vykázanou novopríchodzím objemom telesa. Je odtlačená z cesty telesa, tak na oplátku potlačí iný kus vody, ten zas iný, a takto by to šlo, až kým by sa nejaký do kúta zahnaný kúsok vody nepoddal spoločenskému tlaku a nestlačil sa. Učili nás ale, že voda je ťažko stlačiteľná, a nie je to len taký blud. Skôr ako by sa voda stlačila, vystúpa radšej vyššie, len nech má pokoj. Ak je novopribudnuvší kus telesa objemu \(\Delta V\), rovnaký objem vody sa podeje na vrch. Nás zaujíma hlavne taká vec, o koľko sa zvýši hladina vody oproti pôvodnej (v terminológii Archimedovho zákona: aký kus telesa sa mi ešte navyše ponorí do vody, v teminológii tlakov: o koľko sa ešte navyše zvýši tlak na podstavu).

Pretože sme si tak vhodne zvolili tvar telesa i nádoby, smerodajné parametre sú pre nás veľosti ich podstáv (\(S_0\), resp. \(S\)), a výšku o ktorú zme zatlačili teleso hlbšie v porovnaní s jeho pôvodnou polohou si označme \(x\). Presunutý objem vody je teda \(\Delta V=S_0 x\). Vďaka zvolenej geometrii nám voda na vrchu stúpa v akomsi medzivalcí, a z rovnosti objemov dostávame \(S_0 x=y(S-S_0)\). Na tomto mieste si intenzívnejšie začíname písať rovnice: \[F=-\rho S_0 g (x+y)\text{,}\] \[F=-\rho S_0 g \left(1+\frac{S_0}{S-S_0}\right)\text{,}\] \[F=-\rho S_0 g \frac{S}{S-S_0}x\text{.}\]

Dostali sme výslednú silu v podobe \(F=-kx\) (kde \(k=\rho S_0 g \frac{S}{S-S_0}\)),a jasáme, keďže pre takúto silu (silu od pružiny) je nám už známy výsledok riešenia rovnice kmitov, a to \(T=2\pi\sqrt{\frac{m}{k}}\). Dosadzujeme: \[T=2\pi\sqrt{\frac{m}{\rho S_0 g \frac{S}{S-S_0}}}\]

a upravujeme: \[T=2\pi\sqrt{\frac{m}{\rho S_0 g}}\sqrt{1-\frac{S_0}{S}}\text{.}\]

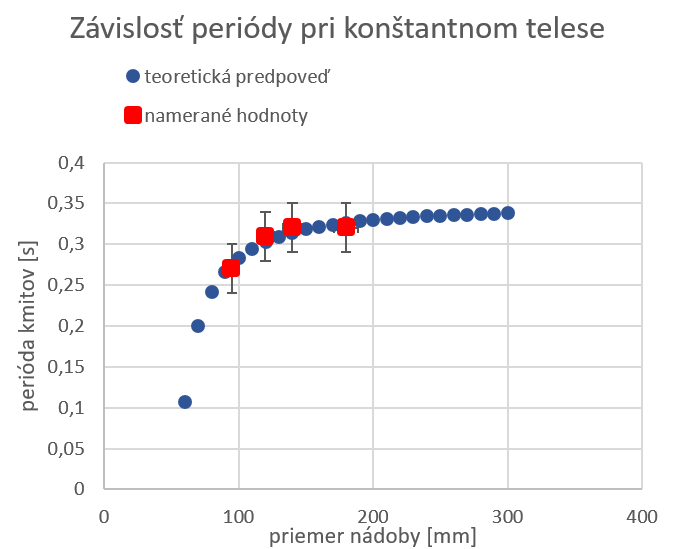
Takže sme sa dopracovali k jednoduchej predpovedi závislosti periódy na veľkosti nádoby. Je namieste sa zamyslieť, ako veľmi je ale táto predpoveď funkčná. I keď nám dáva dobrý predpoklad pre nekonečnú nádobu (skúste si vypočítať periódu kmitov na nekonečnej hladine, stačí len vhodne vynechávať kroky ukázaného riešenia), voda sa nepreskupuje nekonečne rýchlo, a teda nám vznikajú vlny (čo ste mnohí správne uviedli, ale až na výnimky nikto nevybudoval kauzálny reťazec medzi vlnami a zmenou periódy. Vo všeobecnosti je prudentné uvažovať korelácia \(\neq\) kauzalita, t. j. to že sa veci dejú naraz, ešte nutne neznamená, že jedna je (priamo) príčinou/následkom druhej).

Samozrejme že vlny vznikajú i v malých nádobách, ale tam sú maličké, a teda nespôsobujú takú lokálnu zmenu hydrostatického tlaku, aby pozorovateľne zmenili periódu pohybu. O tlmení v závislosti od veľkosti nádoby zatiaľ nevieme povedať veľa, a tak sa už presuňme na samotný experiment.

Tvar používaných nádob a telesa na experiment sme priblížili v teoretickom úvode. Teleso aj vieme rozkmitať vo vertikálnom smere, ostáva nám nejak to merať. Poloha oscilátora je časovo silno závislá vec, a teda je nerozumné žmúriť jedným okom na stopky (perióda) a druhým na pravítko (tlmenie prejavujúce sa klesajúcou amplitúdou). Za najvhodnejšie sa dá považovať analýza videozáznamu experimentu. Pohodlným nástrojom na videoanalýzu je program Tracker.

Spracovanie získaných dát je už podľa ľubovôle, pre názornosť použijeme nejaký tabuľový procesor.

Ako zistíme periódu kmitov? Perióda je definovaná ako časový rozdiel medzi dvoma po sebe idúcimi miestami rovnakej fázy. Takisto ju budeme zisťovať, t. j. nájdeme si (kvôli väčšej presnosti) niekoľko po sebe idúcich miním a odčítame čas, ktorý ich oddeľuje. Ako zistíme tlmiaci koeficient? Nápoveda v zadaní vyjavila exponenciálny pokles amplitúdy kmitov. Ak si k tomu pohľadáme čosi viac, nájdeme, že amplitúda by mala presnejšie vyzerať ako \(A(t)=A_0 e^{-\frac{\gamma}{2}t}\), kde \(A_0\) je počiatočná amplitúda a \(\gamma\) je náš hľadaný tlmiaci koeficient. V skutočnosti ho môžeme zistiť napríklad tak, že po odstránení miním a maxím z našich dát ich skúsime (napríklad pomocou nejakej fitovacej funkcie v tabuľkovom procesore) preložiť exponenciálou, a následne z predpisu fitovacej rovnice vyčítať tlmiaci koeficient.

Ako môžeme vidieť, tlmenie je menej výrazné pri väčších nádobách. Zdôvodniť sa to dá tak, že v menších nádobách mi kmitá väčšiu časť vody pomerne k celku, a teda oscilátor rýchlejšie stráca energiu. Taktiež si môžeme všimnúť, že presnosť experimentu bola výrazne znížená nízkou frekvenciou snímania (len 30 fps).