3. Pomocné kolieska vzorové riešenie

Zadanie

Vo FKS sme sa nedávno hrali s klasickým detským bicyklom s pomocnými kolieskami (takým, kde brzdíte točením pedálov smerom dozadu). Bicykel stál pokojne na zemi, keď tu prišla Tinka a priviazala o pedál, ktorý sa nachádzal v najnižšej možnej pozícii, lanko. Následne potiahla za koniec lanka smerom dozadu. Ktorým smerom sa bicykel pohol, a prečo?

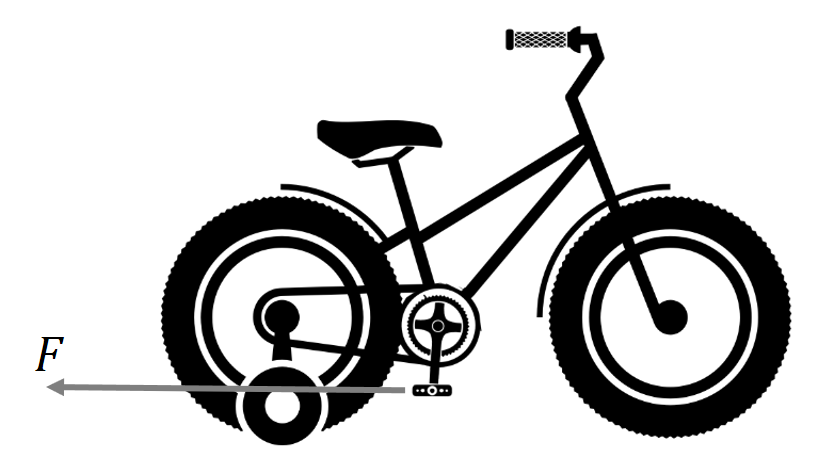
Táto úloha sa ukázala ako skutočne divotvorná, hoci otvorene vyhlasujeme, že nebola ťažká. Primitívnym a pritom dobrým riešením bolo proste zobrať bicykel a skúsiť to – aj menej bystrý riešiteľ tak mohol prísť na to, že sa bicykel pohne dozadu.¹ I tak by sa však patrilo k tomu dopísať niekoľko teplých slov a fyzikálne to zdôvodniť. Teoretici však bicykle z princípu nemajú, takže si museli vystačiť s úvahou. Ani tá však nebola nijak ťažká.

Takže sa pozrime najskôr na to, aké vonkajšie sily na náš bicykel pôsobia. Vo vertikálnom smere sú to tiažová sila a normálové sily od podložky pôsobiace na kolesá bicykla, ktoré kompenzujú práve tiaž bicykla. Je teda zjavné, že vo zvislom smere sa nič zaujímavé diať nebude. Koľké to prekvapenie.

Čiže budeme skúmať len horizontálny smer. Tam je to sila \(\vec{F}\), ktorou ťaháme za pedál smerom dozadu a trecie sily medzi kolesami a podložkou. Trecie sily pôsobia vždy proti smeru pohybu. V prípade, že kolesá neprešmykujú, pre ich veľkosti platí \(F_t \leq\mu_s N\), kde \(N\) je veľkosť normálovej sily medzi kolesom a podložkou.

Teraz potiahnime pedál dozadu nejakou silou, dostatočne malou na to, aby koleso nezačalo prešmykovať, a zamyslime sa nad tým, čo sa stane. Keby sme zadné koleso nadvihli tak, aby sa nedotýkalo podložky, potom by sme jasne videli, že sa roztočí tým istým smerom, ako pedál. Preto intuitívne očakávame, že keby bol bicykel položený na podložke, mal by sa pohybovať smerom dopredu. No nerobme unáhlené závery.

Najprv si predstavme, že pôsobisko sily \(\vec{F}\) je nekonečne blízko k osi otáčania pedálu. Moment tejto sily je v limite rovný nule. To ale znamená, že nespôsobuje otáčanie pedálom, a teda výsledný efekt je taký, ako keď ťaháme priamo za bicykel, čiže bicykel pôjde dozadu.²

Na druhej strane uvažujme veľmi dlhý pedál.³ V takom prípade aj malá sila dokáže vyvinúť dostatočne veľký krútiaci moment, takže dominantné bude práve roztáčanie pedála a bicykel sa bude pohybovať smerom dopredu.

Už by ste mali tušiť, že pre nejakú dĺžku pedála bude bicykel stáť na mieste. Otázne je, či reálna dĺžka pedála je kratšia alebo dlhšia ako hraničná dĺžka, a teda či bicykel pôjde dozadu alebo dopredu. Pre reálny hmotný bicykel sa k odpovedi žiadnou jednoduchou úvahou nedopracujeme, budeme musieť počítať. Ak si ale povieme, že kolesá, reťaz, šnúrka a ostatné príslušenstvo sú ľahké, úloha sa redukuje na jednoduché páky. Ďalej zatiaľ uvažujme vysoké trenie, teda že nám zadné koleso nebude prešmykovať.

Takže si teda relevantné rozmery zakreslime. Zistíme, že stačí vziať do pomeru dĺžku pedálu \(r\), polomer kolesa \(R\) a počty zubov na pastorkoch vpredu a vzadu, \(k_1\) a \(k_2\). Vyjde nám, že sila, ktorou zadné koleso poháňa bicykel vpred, je \(F (r k_2) / (R k_1)\). Označme si tento koeficient \(\gamma\). Čiže máme silu \(F\), ktorá ťahá bicykel dozadu, a silu \(\gamma F\), ktorá sa ho snaží hnať vpred. Odčítame ich a bude nám hneď jasné, že bicykel tlačí dopredu celková sila \(F(\gamma - 1)\). Takže ak

• \(\gamma < 1\), bicykel bude chcieť ísť dozadu,
• \(\gamma = 1\), bicykel sa nepohne,
• \(\gamma > 1\), bicykel pôjde dopredu.

Ako sme si povedali, pre neakademické bicykle je pomer \(r/R < 1\), reálna hodnota je okolo \(\num{0.5}\). Pomer počtu zubov sa zas zvykne pohybovať rádovo okolo jednej.⁴ Dokonca úplne stačilo považovať počty zubov za rovnaké, u bicykla s pomocnými kolieskami je to jedno. Potom ostane iba pomer dĺžky pedála a polomeru kolesa a na tom vidno krásne. Skutočné zrýchlenie bicykla však nijak jednoducho nenájdeme, závisí totiž od mnohých ďalších parametrov.⁵

Úvaha nad cykloidami

Iným spôsobom riešenie je uvedomiť si, aké sú všetky možné pohyby pedálu. Pekne spracovanú názornú ukážku môžete nájsť tu: https://www.youtube.com/watch?v=aJhiY70KY5o.

Vidíme, že ak bicykel neprešmykuje, koniec pedála je v sústave Zeme viazaný na krivku zvanú cykloida.⁶ Pohybovať sa smie iba dopredu-dozadu po nej a nikdy inak. Pohybové rovnice stále platia, ale silu pôsobiacu na pedál musíme najprv kolmo premietnuť do smeru dotyčnice k tejto krivke – kolmé zložky majú smolu, väzba ich proste zruší.

No a teraz by už malo byť jasné, že podľa toho, aký je pomer \(\gamma\), rozoznáme tri prípady:

• skrátená cykloida: \(\gamma < 1\), bicykel pôjde dozadu,
• prostá cykloida: \(\gamma = 1\), bicykel sa nepohne, lebo zo zadania sa pedál nachádza práve naspodku krivky,
• predĺžená cykloida: \(\gamma > 1\), bicykel sa pohne vpred (ale iba do momentu, kým nedosiahne najľavejšiu časť slučky).

Z videa taktiež vidno, že ak by sme lankom neťahali rovno dozadu, ale šikmo, kolmý priemet sily do tejto cykloidy môže niekedy smerovať smerom dopredu, dokonca aj v prípade reálneho bicykla s \(\gamma < 1\). A naozaj, ak dáme pedál šikmo dozadu dolu a ťaháme šikmo dozadu hore, bicykel sa zrazu ochotne šinie vpred v ústrety svetlým zajtrajškom.

Prešmykovanie

Nakoniec sa zamyslime nad tým, čo sa stane, ak budeme zväčšovať silu, ktorou za pedál ťaháme. Od istého momentu sa koleso nebude stíhať roztáčať, a začne prešmykovať. V tomto novom prípade presne poznáme veľkosť trecej sily \(F_{t}=\mu_{d}N\). V hrubom priblížení možno povedať, že smer pohybu bude potom dozadu, aj keď v skutočnosti výpočet nás dovedie ku komplexnejšiemu vzťahu, kde sa ukáže závislosť na parametroch bicykla.

Komentár k riešeniam

Bol som dosť prekvapený, aké ťažkosti dokázala táto úloha vyrobiť, či už medzi vami alebo vedúcimi – naozaj sme sa dlho nevedeli zhodnúť, ako to vlastne v skutočnosti je. Našťastie skutočný bicykel spory rýchlo rozhodol a pekné hĺbkové vysvetlenie s cykloidami sa dalo nájsť vo videu na YouTube. Jaro vytvoril detailnú analýzu pre hmotný bicykel, ktorá však silne prekračovala očakávanú úroveň obtiažnosti.

Za správnu odpoveď „dozadu“ boli spravidla obratom udelené tri body, za dobré vysvetlenie zvyšných šesť, prípadne nejaká pomerná časť za väčšie nezrovnalosti. Za drobné nepresnosti nešlo dolu zväčša nič, maximálne som si trochu súkromne zagrúlil a následne napísal deviatku. Ale neznamená to, že si na tom do budúcna nemáte dať záležať.

Špeciálne pekné riešenia prišli od Elišky Macákovej (premiestnenie pedálu na os zadného kolesa, kde odpoveď vidno okamžite), Katky Dančejovej, Dávida Mišiaka a Martina Števka.