Zadanie
Maťo sa tento polrok naplno pustil do štúdia špeciálnej teórie relativity. V nej ho zaujala taká filozofická otázka, na ktorú by rád od vás počul odpoveď. Vedeli by ste Maťovi vysvetliť, ako medzi sebou súvisí fakt, že transformácia polohy a času (tzv. Lorentzove transformácie) sú medzi dvoma inerciálnymi vzťažnými sústavami lineárne1 s faktom, že nevieme žiadnym experimentom (ani len myšlienkovým) rozlíšiť medzi dvoma inerciálnymi vzťažnými sústavami2 (tým máme na mysli, že všetky fyzikálne zákony vyzerajú v oboch inerciálnych vzťažných sústavách rovnako)?
Nuž, filozofické otázky nechajme filozofom a skúsme sa na to pozrieť ako fyzici. Skúsme začať z toho čo poznáme, a to ako sa súradnice menia pri obyčajnom posune.
Predstavme si, že máme v priestore dva body, \(A\) a \(B\) a snažíme sa zmerať vzdialenosť medzi týmito bodmi v rôznych vzťažných sústavách. Prvá sústava, \(S\), je v pokoji a má počiatok v bode \(A\). Pozorovateľ v tejto sústave teda vidí že vzdialenosť medzi \(A\) a \(B\) je \(l\). Teraz sa presunieme do sústavy \(P\), ktorá je stále v pokoji, ale posunutá o vzdialenosť d od sústavy \(S\). V sústave \(P\) stále vidíme, že \(A\) je od \(B\) vzdialené práve \(l\).
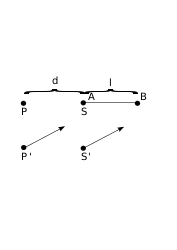
Čo by sa však stalo, ak by sa tieto sústavy zmenili na také, ktoré majú počiatok na rovnakom mieste, ale obe sa hýbu konštantnou rýchlosťou rovnakým smerom, teda \(P \rightarrow P'\), \(S \rightarrow S'\), ako na obrázku? Vieme, že presun medzi dvoma sústavami nám zmení priestor podľa nejakej funkcie, nazvime ju \(g\). Teda, ak poloha bodu \(B\) v sústave \(S\) bola \(l\), tak poloha bodu \(B\) v sústave \(S'\) bude \(g(l)\).
| \(A\) | \(B\) | \(B-A\) | |
|---|---|---|---|
| \(S\) | \(0\) | \(l\) | \(l\) |
| \(P\) | \(d\) | \(d+l\) | \(l\) |
| \(S'\) | \(0\) | \(g(l)\) | \(g(l)\) |
| \(P'\) | \(g(d)\) | \(g(d+l)\) | \(g(d+l)-g(l)\) |
Sústavy \(S'\) a \(P'\) sú však stále iba posunuté vzhľadom na seba, a teda dĺžky v nich zmerané sa musia rovnať. Teda platí \[ g(l) = g(d+l) - g(l)\text{.} \]
Z tohoto už môžeme vidieť, že naša transformácia \(g\) musí byť lineárna. Napríklad ak by sme túto rovnicu zderivovali (pozerali sa, ako sa zmení hodnota funkcie pri malej zmene parametra \(l\)) podľa \(l\), dostali by sme rovnosť
\[ g'(l) = g'(d+l)\text{.} \]
Táto podmienka nám len hovorí, že v každom bode musí funkcia rásť rovnako rýchlo (derivácia má byť konštantná). Takúto podmienku spĺňa jedine lineárna funkcia.
Zatiaľ sme sa celý čas rozprávali iba o závislosti priestorovej transformácie od priestoru. Čo však nesmieme zabudnúť je, že priestorová transformácia môže závisieť aj od času, teda celá transformácia má tvar \(x' = h(t) x + g(t)\). To sme zatiaľ zjednodušili na tvar \(x' = a x + g(t)\)1. Už vieme, že \(a\) je konštanta a jediné, čo teraz potrebujeme zistiť je, či aj \(g(t)\) je lineárna funkcia.
Vieme, že relatívna rýchlosť dvoch vzťažných sústav musí byť zachovaná, pretože inak by sme porušili podmienku, že sústavy sú inerciálne. Ak by však naša transformácia závisela od času nelineárne, táto relatívna rýchlosť by sa nezachovávala. Teda vieme, že aj tento komponent transformácie musí byť lineárny.
Týmto sme teda vyriešili transformáciu priestorových súradníc, avšak stále nám chýba časť, ktorá by transformovala časovú súradnicu. Našťastie, tak ako sme vedeli odvodiť transformáciu priestorových súradníc len vďaka tomu, že vieme, ako sa súradnice menia priestorovým posunom, úplne rovnako vieme, ako sa časové súradnice menia časovým posunom. A teda vieme úplne rovnaký argument zopakovať2 aj pre linearitu časových transformácií.
Na záver sa teda ešte skúsme zamyslieť, ako by sa prejavila prípadná nelineárnosť transformácie súradnic. Využijeme znovu trik so sústavami vzdialenými o nejaké \(d\). Na pomoc si môžeme zobrať pravítko, na ktorom sa, ako sa na správne pravítko patrí, nachádzajú v pravidelnom intervale značky. Ak by transformácia súradníc nebola lineárna, relatívna vzdialenosť značiek by sa menila, to by ale znamenalo, že vieme rozlíšiť medzi dvomi inerciálnymi sústavami, čo by ale bolo v spore s predpokladom teórie relativity (to, či je tento predpoklad správny, fyzici prakticky testujú tak, či produkuje experimentálne a teoreticky konzistentné výsledky).
Ak sa vzájomná rýchlosť sústav nemení, koeficient \(a\) nemôže závisieť od času. Veríme totiž, že fyzikálne zákony by nemali záležať od toho, od akého okamihu meriame čas. Ak by \(a\) záviselo od času, aj keby bola vzájomná rýchlosť dvoch sústav rovnaká, dalo by sa to spozorovať.↩
V krátkosti, stačí v predošlej úvahe vymeniť priestor za čas a všetky priestorové intervaly za časové a celá úvaha zostane v platnosti.↩
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.