5. Kajkin model trenia vzorové riešenie

Zadanie

Kajka sa na poslednom sústredku dozvedela, že trenie je vlastne to, čo umožňuje ísť okrúhlym veciam vpred. Doma si to chcela otestovať, a tak vzala valček polomeru \(R\) zo stavebnice, nechala ho kotúľať a na oštaru zistila, že spomaľuje.

Keďže Kajka je motivovaná, rozhodla sa preraziť na poli teoretickej fyziky a prišla s vlastným modelom valivého trenia. Predstavila si, že ten valček je vlastne hranol s podstavou pravidelného \(N\)-uholníka a vypočítala, koľko energie sa stratí pri prevaľovaní cez hrany. Pre jednoduchosť si povedala, že pri prevalení cez hranu sa po dopade hranola na podložku všetka energia potrebná na prevalenie premení na teplo.

Aký by musel byť koeficient šmykového trenia pri šmýkaní kvádra rovnakej hmotnosti o podložku, aby spomaľoval rovnako ako Kajkin hranol? Bude tento model trenia fungovať aj pre nekonečné \(N\)?

V prvom rade sa musíme rozhodnúť, ako aproximujeme valec hranolom. Hranol môžeme vpísať do valca, môžeme ho opísať valcu, no môžeme si vybrať aj ľubovoľnú polohu z intervalu týchto dvoch krajných polôh. Vo vzoráku budeme detailne skúmať prípad, keď hranol do valca vpíšeme, a potom len stručne uvedieme, aké výsledky by sme dostali, keby sme mu ho opísali. Ale poďme pekne po poriadku.

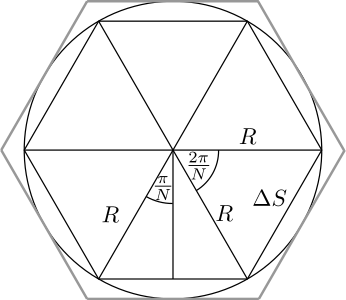
Najskôr si vypočítajme, akú energiu spotrebujeme pri prevalení hranola cez hranu. Uvažujme hranol s podstavou pravidelného \(N\)-uholníka. Rozdeľme si hranol na \(N\) zhodných trojbokých hranolov, ktorých podstavami sú rovnoramenné trojuholníky s uhlom oproti základni veľkosti \(\frac{2\pi}{N}\) a ramenami dĺžky \(R\). Keď hranol leží na podložke, jeho ťažisko je vo výške \(R\cos\frac{\pi}{N}\) nad podložkou. Pri prevaľovaní sa dostane do maximálnej výšky \(R\), preto je na prevalenie potrebná energia aspoň \[\Delta E=MgR\left(1-\cos\frac{\pi}{N}\right)\textrm{.}\] Po každom prevalení hranol stratí túto energiu (podľa zadania sa všetka premení na teplo). Ak hranol nemá túto energiu, už sa ďalej nemôže prevaľovať a spadne späť, kde zostane stáť.¹ Pri každom prevalení sa hranol posunie ďalej o dĺžku základne trojuholníka \[\Delta s=2R\sin\frac{\pi}{N}\text{.}\]

Zodpovedzme najskôr otázku, či tento model funguje aj pre nekonečné \(N\). Jednému otočeniu valca zodpovedá \(N\) prevalení, a preto sa spotrebuje celková energia²

\[N\Delta E=\left|NMgR\left(1-\cos\frac{\pi}{N}\right)\right|_{N\rightarrow\infty}=MgR\underset{N\rightarrow\infty}{\lim}\frac{\pi^{2}}{2N}=0\text{.}\] Vidíme, že v limitnom prechode, keď \(N\) ide do nekonečna, sa pri jednom otočení valca nespotrebuje žiadna energia, a teda valec nebude spomaľovať. To znamená, že musíme uvažovať nejaké konkrétne, dostatočne veľké, no konečné \(N\), aby sme hranolom dostatočne presne aproximovali valec, no zároveň, aby model trenia ešte stále fungoval.

Udeľme valcu rýchlosť \(v_{0}\). To znamená, že má energiu \[E_{0}=E_{k}+E_{r}=\frac{1}{2}Mv_{0}^{2}+\frac{1}{2}J\omega_{0}^{2}=\frac{1}{2}\left(M+\frac{J}{R^{2}}\right)v_{0}^{2}\text{,}\] kde \(J\) je moment zotrvačnosti hranola. Pre dostatočne veľké \(N\) možno uvažovať, že sa len málo líši od valca, a teda možno položiť \(J\approx\frac{1}{2}MR^{2}\).³

Nech má teda valec energiu \(E_{0}\). To znamená, že dôjde k \(\left\lfloor \frac{E_{0}}{\Delta E}\right\rfloor\) prevaleniam a valec pred tým, než zastane, prejde vzdialenosť \(s=\left\lfloor \frac{E_{0}}{\Delta E}\right\rfloor \Delta s\).⁴ Dosaďme do tohto vzťahu príslušné výrazy. V priblížení \(J\approx\frac{1}{2}MR^{2}\) dostávame⁵ \[s=\left\lfloor \frac{\frac{3}{4}Mv_{0}^{2}}{MgR\left(1-\cos\frac{\pi}{N}\right)}\right\rfloor 2R\sin\frac{\pi}{N}\approx\frac{\frac{3}{4}v_{0}^{2}}{gR\frac{\pi^{2}}{2N^{2}}}2R\frac{\pi}{N}=\frac{3N}{\pi}\frac{v_{0}^{2}}{g}\text{.}\]

Pre záujemcov uveďme aj výsledok, ktorý by sme dostali, keby sme uvažovali exaktný vzťah pre moment zotrvačnosti hranola. S využitím uvedených priblížení by sme dostali \(s\approx\left(\frac{3N}{\pi}-\frac{2\pi}{3N}\right)\frac{v_{0}^{2}}{g}\).

Teraz už len zostáva porovnať tento výsledok s výsledkom pre šmykové trenie. V prípade šmykového trenia je za spomaľovanie zodpovedná konštantná trecia sila veľkosti \(F_{t}=fMg\), teda zrýchlenie má veľkosť \(a=fg\). Napíšeme kinematické rovnice pre rovnomerne spomalený pohyb \(s=v_{0}t-\frac{1}{2}at^{2}\) a \(v=v_{0}-at\). Vylúčením času z rovníc dostávame \(s=\frac{v_{0}^{2}-v^{2}}{2a}\). Zaujíma nás dráha, na ktorej kváder zastane, preto položme \(v=0\) a dostaneme \[s=\frac{v_{0}^{2}}{2a}=\frac{v_{0}^{2}}{2fg}\text{.}\]

Porovnajme tento výsledok s výsledkom pre Kajkin model. Dostaneme potom podmienku \[f\approx\frac{\pi}{6N}\] ak počítame s momentom zotrvačnosti pre valec,⁶

Uveďme ešte v skratke, čo by sme dostali, keby sme uvažovali aproximáciu hranolom opísaným valcu. Energia potrebná na jedno pretočenie v tomto prípade je \(\Delta E=MgR\left(\frac{1}{\cos\frac{\pi}{N}}-1\right)\) a posunutie pri každom prevalení \(\Delta s=2R\tan\frac{\pi}{N}\). V limitnom prechode pre \(N\) idúce do nekonečna dostávame energiu potrebnú na jedno otočenie valca \(N\Delta E=\left.NMgR\left(\frac{1}{\cos\frac{\pi}{N}}-1\right)\right|_{N\rightarrow\infty}=MgR\underset{N\rightarrow\infty}{\lim}\frac{N\pi^{2}}{2N^{2}-\pi^{2}}=0\), čiže opäť dostávame, že ani v tomto prípade Kajkin model nefunguje. V priblížení \(J\approx\frac{1}{2}MR^{2}\) dostávame prejdenú vzdialenosť tak isto \(s\approx\frac{3N}{\pi}\frac{v_{0}^{2}}{g}\), a teda \(f\approx\frac{\pi}{6N}\).⁷