2. Piatok večer na kanoe vzorové riešenie

Tak sme zasa raz skúsili, ako sa viete vynájsť, keď je cieľom úlohy niečo odmerať… a tentokrát sa to dokonca obišlo aj bez bravčového karé.

V 17. storočí už zemský polomer samozrejme odmeraný bol, a dokonca celkom presne. Stačilo zobrať nejaký už vynájdený prístroj na meranie uhlov, napríklad kvadrant alebo astrolábium. Precízna technika sa však zvykne vyznačovať slabou odolnosťou voči stroskotaniu, takže Robinson s Piatkom zrejme nič také nemajú, no a žeby ľudožrúti používali zvyšné kosti z obeda na zostrojovanie astronomických pomôcok sa takisto nedá očakávať. Lenže zemský polomer v skutočnosti šlo odmerať už v staroveku, a s trochou dôvtipu mohol niektoré z navrhnutých metód použiť dokonca už aj praveký človek.

Máme more aj Slnko

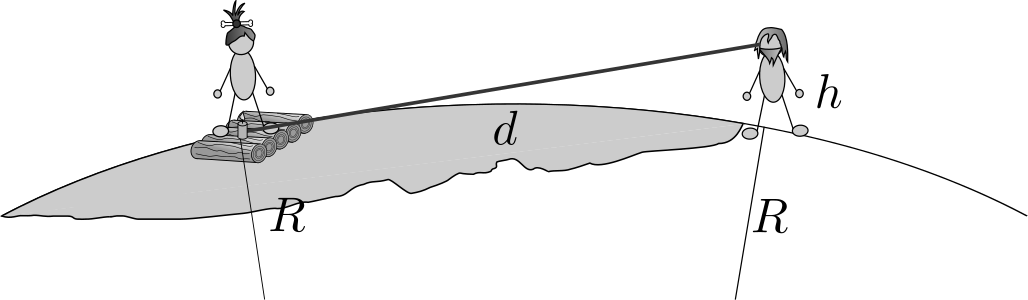
Ak máme aj more, aj Slnko (a povedzme, že existuje dôvodný predpoklad, že Robinson a Piatok oboje mali), dá sa vymyslieť všeličo. Jedna elegantná metóda vyzerá takto: posadíme Piatka na západný breh ostrova tak, aby mal oči tesne nad hladinou, a Robinsona pošleme na blízky kopec známej výšky. Výškový rozdiel \(h\) nie je ťažké odmerať – medzi obomi bodmi napneme špagát a odmeriame pásmom, akú výšku prekonal na dĺžke jedného metra. Keď zmeriame celkovú dĺžku špagáta, trojčlenkou ľahko zistíme, o koľko vyššie sú Robinsonove oči. Potom stačí počkať na západ Slnka. Ako taký západ vyzerá? Zem sa postupne otáča a unáša body na svojom povrchu smerom do tieňa. Táto hranica medzi svetlom a tieňom sa odborne nazýva terminátor.

Piatkovi slnko zapadne v momente, keď jeho hlava prejde terminátorom, sváko Robinson ho však z kopca bude vidieť až do chvíle, keď terminátorom prejde jeho horizont. Kopec samozrejme musí byť buď dosť strmý na to, aby sme mohli vodorovnú vzdialenosť zanedbať, alebo by mal byť kolmo vzhľadom na Slnko od miesta, kde sedí Piatok. Z časového rozdielu západov Slnka \(t\) vieme zistiť uhol \(\alpha\) medzi horizontami oboch experimentátorov meraný od stredu Zeme. Stačí zobrať pomer \[ \frac{t}{\text{jeden deň}} = \frac{\alpha}{2\pi\ (\text{čiže } \ang{360})}. \]

Robinson teda vie, že za čas \(t\) sa Zem otočí o toľko, ako ďaleko dovidí z výšky \(h\). Túto vzdialenosť síce nepoznáme, ale z obrázka vieme určiť, že \[ \cos{\alpha} = \frac{R}{R + h}, \] odkiaľ úpravami dostaneme \[ R = h \cdot \frac{\cos{\alpha}}{1 - \cos{\alpha}} = h \cdot \frac{ \cos{(2\pi \cdot \frac{t}{\SI{86400}{\second}})} }{ 1 - \cos{(2\pi\cdot\frac{t}{\SI{86400}{\second}})} }. \]

Ostáva nám ale ešte spomenúť jednu vec: celý čas sme predpokladali, že Slnko zapadá do mora kolmo. To nemusí byť vždy pravda, našťastie Piatok s Robinsonom sú dostatočne blízko rovníka, takže im to príliš veľkú chybu nevyrobí (a keby aj, meraním rozdielu polohy prvého a posledného kontaktu Slnka s horizontom sa to dá opraviť, rozmyslite si ako).

Pre porovnanie s realitou: ak by Robinson vyliezol na stometrový kopec, jeho horizont bude vzdialený približne \(\SI{36}{\kilo\metre}\), čo je asi tretina stupňa zemepisnej šírky alebo \(\frac{1}{3 \cdot 360} = \frac{1}{1080}\) obvodu Zeme. Slnko by mal teda vidieť približne o minútu a štvrť dlhšie, než Piatok. Pri takomto výškovom rozdieli je skutočne možné zemský polomer odmerať veľmi presne aj bez stopiek.

More máme, ale je zamračené

Teoreticky to spravíme takto: počkáme na pokojnú hladinu, Piatka večer posadíme na kanoe a pošleme ho, nech vesluje, až kým nezmizne Robinsonovi, stojacemu na brehu, z dohľadu. Zo zakrivenia Zeme by sme potom mali vedieť určiť aj jej polomer.

Pravda, musíme vyriešiť zopár technických detailov. Napríklad je ťažké presne určiť, či ešte kanoe stále vidíme. Preto pribalíme Piatkovi sviečku. V noci budeme vedieť presne povedať, či ju ešte vidíme, alebo už nie.

Rovnako by sme potrebovali poznať presnú výšku sviečky nad hladinou a tiež výšku Robinsonových očí, tie však vieme odmerať alebo nastaviť, ako potrebujeme. Tak napríklad sviečku umiestnime na kanoe presne dva metre nad hladinu, a Robinson si sadne do vody tak, aby mal oči tesne nad hladinou. Alebo miesto kanoe použijeme placatú plťku¹, sviečku dáme niekam do stredu a Robinson sa postaví tak, aby mal oči v známej výške nad hladinou. Dva metre sú fajn, jeho horizont je potom v realistickej vzdialenosti \(\SI{5.1}{\kilo\metre}\).

Samozrejme, nestačí vedieť, kedy svetielko zmizlo, ale musíme poznať presnú vzdialenosť loďky od brehu. Tu je však pomoc ľahká… kanoe priviažeme na dlhý motúz a zaznačíme si, koľko z neho sa odvinulo. Ak by sme náhodou nenašli dostatočne dlhý motúz, môžeme to urobiť ešte inakšie, aj keď za cenu podstatne nižšej presnosti. Môžeme použiť napríklad dve pušky (každému dáme jednu). Keď svetielko zmizne, Robinson vystrelí zo svojej. Keď Piatok začuje výstrel, odpovie mu rovnako, a zo známeho oneskorenia spočítame vzdialenosť ako \(d = v\Delta t/2\).

Mohli by sme namietnuť, že Robinson s Piatkom možno nepoznajú rýchlosť zvuku. Než by sa však stihli zase do krvi pohádať a odplašiť aj zvyšok ostrovnej fauny, prezradíme im, že si ju môžu odmerať. Stačí rovnaký experiment vykonať na súši, kde si vzdialenosť môžu odkrokovať alebo odmerať pásmom.

Keď už poznáme vzdialenosť k horizontu \(d\), polomer dopočítame z Pytagorovej vety \[ \left(R + h\right)^2 = R^2 + d^2. \]

Toto si rozpíšeme a malý člen \(h^2\) zanedbáme (lebo \(h\) je omnoho menšie, než \(R\)), ostane nám \[ R = \frac{d^2}{2h}. \]

Nemáme more, ale je jasno

Meranie sa dá úspešne vykonať aj vtedy, keď more nemáme (alebo je hrozne rozbúrené). Známym príkladom už zo staroveku je metóda, ktorú vyhútal strýco menom Eratostenes: všimol si, že v meste Syene (dnešný Asuán v Egypte) majú studňu, do ktorej v deň letného slnovratu Slnko svieti zvislo zhora. V Alexandrii, ktorá je o niečo severnejšie, to už však nešlo – Slnko nikdy na oblohe nevystúpilo až do zenitu. Eratostenes si uvedomil, že ak presne odmeria poludníkovú vzdialenosť medzi týmito dvomi mestami a uhly, pod ktorými Slnko vrhá tiene na poludnie v rovnaký deň, bude vedieť zistiť, aký je jej obvod a teda aj polomer.

Takže sa pokúsime Eratostenovu metódu aplikovať v malej škále, zato s trochu lepšou presnosťou, aká sa dala dosiahnuť so studňou. Najprv potrebujeme zistiť, ktorým smerom je sever. To je ľahké, stačí nám nájsť Polárku alebo odmerať azimut východu a západu Slnka a nájsť stred medzi nimi. Potom niektorou zo spomenutých metód odmeriame čo najväčšiu vzdialenosť v tomto smere – povedzme, že dvadsať kilometrov zvládneme a ešte nevybehneme z ostrova. Pravdaže, tieto dve miesta nemusia ležať presne na poludníku, dôležitá je iba ich vzájomná severo-južná vzdialenosť.

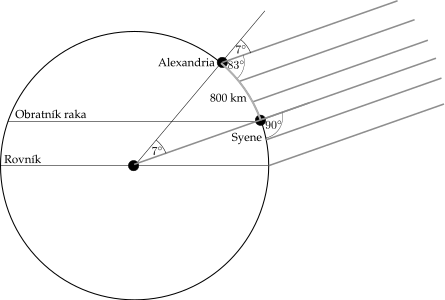
Následne na každom z týchto miest zavesíme olovnicu a počkáme, kým Slnko vystúpi na najvyšší bod svojej zdanlivej dráhy, čiže na poludnie. Vtedy odmeriame dĺžku tieňa olovnice a z nej zistíme uhlovú výšku Slnka nad obzorom na oboch miestach, \(\beta_1\) a \(\beta_2\). Najlepšie bude, ak každý pôjde na iné miesto a meranie vykonajú v ten istý deň, keďže výška Slnka nad obzorom je v rôzne dni rôzna. Teraz nám bude stačiť jednoduchá úvaha: poznáme rozdiel uhlov \(\beta_1 - \beta_2\) a vieme, akej skutočnej vzdialenosti zodpovedá. Trojčlenkou ľahko získame obvod Zeme a delením \(2\pi\) dostaneme jej polomer.

Nemáme ani more, ani Slnko

Tu to už začína byť náročné. Ak je jasná noc, môžeme spraviť niečo podobné, ako v minulom prípade: miesto Slnka použijeme niektorú hviezdu a namiesto tieňa budeme sledovať jej vzdialenosť od vodorovnej roviny pri jej dolnej kulminácii².

Na určenie vodorovnej roviny nám bude stačiť mištička s vodou. Sextant síce nemáme, ale ak sa zvolená hviezda približuje dosť blízko k horizontu, Piatok môže napríklad použiť svoju obľúbenú kľúčnu kosť z portugalského námorníka, ktorý kedysi stroskotal na vedľajšom ostrove.³ Ak ju bude držať v natiahnutej ruke, pomocou pásma a jednoduchej trigonometrie môže zistiť, aký uhol mu zaberá v zornom poli.

Alebo opäť použijeme olovnicu – Robinson si pod ňu ľahne tak, aby mal oko presne pod závažím. Potom bude už len čakať, kým mu presne ponad hlavu (teda spojnicu špičky olovnice a jej závesu) neprejde nejaká hviezda. Ďalšiu noc sa prejde na druhé vybrané miesto o niečo severnejšie a znovu počká na tú istú hviezdu aj s olovnicou. Teraz by mal vidieť, že hviezda už neprejde zenitom, ale kúsok vedľa. Piatkovou metódou odmeria tento maličký uhol a je vybavený. Uhol síce bude v skutočnosti dosť malý (rádovo jeden stupeň na 111 kilometrov), ale ak bude olovnica dosť dlhá, meranie by malo vyjsť. Pravda, presnosť bude pomerne nízka.

Nemáme ani hviezdy

Čo však robiť, ak je zamračená noc a more je veľmi rozbúrené? Prvou odpoveďou môže byť aj „sadnúť si na najbližší placatý kameň a plakať“, lebo tu už to naozaj jednoduché nebude. Druhá odpoveď však bude, že sa to stále dá, aj keď presnosť nebude veľmi veľká.

Vyjdeme z toho, že aj keď nemáme nejaký globálny horizont, stále vieme určiť vodorovnú rovinu lokálne, napríklad pomocou misky s vodou. Piatok aj Robinson si zoberú každý jednu misku a odídu každý na iné miesto – tak, aby sa navzájom videli a aby ich nadmorské výšky boli aspoň približne rovnaké. Dobre poslúži dlhé piesčité pobrežie alebo dve úbočia nejakej širokej doliny. Pred začiatkom experimentu ešte niektorým z vyššie popísaných spôsobov určia svoju vzájomnú vzdialenosť. Potom každý u seba postaví malú vežičku (ak budú od seba povedzme , bude stačiť asi dvojmetrový kolík).

Robinson postaví svoju misku na zem a naleje do nej vodu až po okraj. Tým určí dotyčnú rovinu k Zemi. Potom priloží oko alebo ďalekohľad k hladine tak, aby videl iba to, čo sa deje nad ňou a dá signál Piatkovi (napríklad výstrelom z pušky, alebo odpáli trochu pušného prachu…). Piatok začne veľmi pomaly spúšťať sviečku z vrchola svojej vežičky. Keď sviečka Robinsonovi zmizne z dohľadu, znovu vystrelí z pušky a Piatok si urobí na svojom stĺpe značku. Potom to isté vykonajú aj v opačnom smere a dostanú situáciu ako na obrázku:

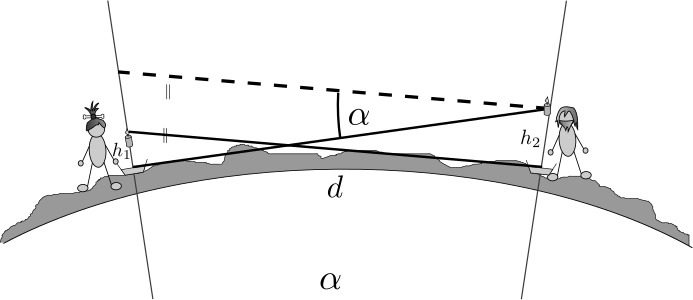
Odtiaľ im stačí vyjadriť súčet výšok \(h_1\) a \(h_2\), a už by sme mali vidieť, že v priblížení malých uhlov platí \[ \frac{h_1 + h_2}{d} = \tan{\alpha} \approx \alpha. \]

No a z \(\alpha\) a \(d\) už polomer \(R\) získame rovnako ako vyššie trojčlenkou.